Solving a difficult physics problem can be surprisingly similar to assembling an interlocking mechanical puzzle. In both cases, the particles or pieces look alike, but can be arranged into a beautiful structure that relies on the precise position of each component (Fig. 1). In 1983, the physicist Robert Laughlin made a puzzle-solving breakthrough by explaining the structure formed by interacting electrons in a device known as a Hall bar1. Although the strange behaviour of these electrons still fascinates physicists, it is not possible to simulate such a system or accurately measure the particles’ ultrashort time and length scales. Writing in Nature, Clark et al.2 report the creation of a non-electronic Laughlin state made of composite matter–light particles called polaritons, which are easier to track and manipulate than are electrons.
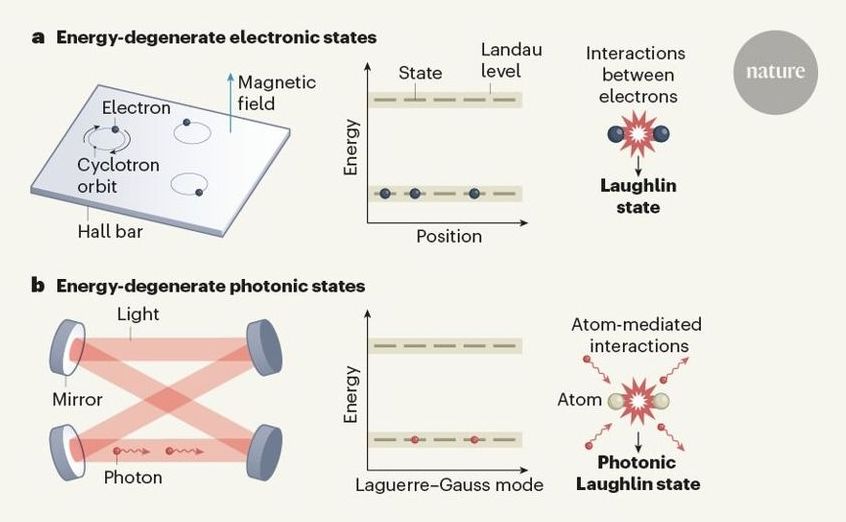
To picture a Laughlin state, consider a Hall bar, in which such states are usually observed (Fig. 2a). In these devices, electrons that are free to move in a two-dimensional plane are subjected to a strong magnetic field perpendicular to the plane. In classical physics, an electron at any position will start moving along a circular trajectory known as a cyclotron orbit, the radius of which depends on the particle’s kinetic energy. In quantum mechanics, the electron’s position will still be free, but its orbital radius — and, therefore, its kinetic energy — can be increased or decreased only in discrete steps. This feature leads to large sets of equal-energy (energy-degenerate) states called Landau levels. Non-interacting electrons added to the lowest-energy Landau level can be distributed between the level’s energy-degenerate states in many different ways.
Adding repulsive interactions between the electrons constrains the particles’ distribution over the states of the lowest Landau level, favouring configurations in which any two electrons have zero probability of being at the same spot. The states described by Laughlin have exactly this property and explain the main features of the fractional quantum Hall effect, whereby electrons in a strong magnetic field act together to behave like particles that have fractional electric charge. This work earned Laughlin a share of the 1998 Nobel Prize in Physics. Laughlin states are truly many-body states that cannot be described by typical approximations, such as the mean-field approximation. Instead, the state of each particle depends on the precise state of all the others, just as in an interlocking puzzle.









Comments are closed.