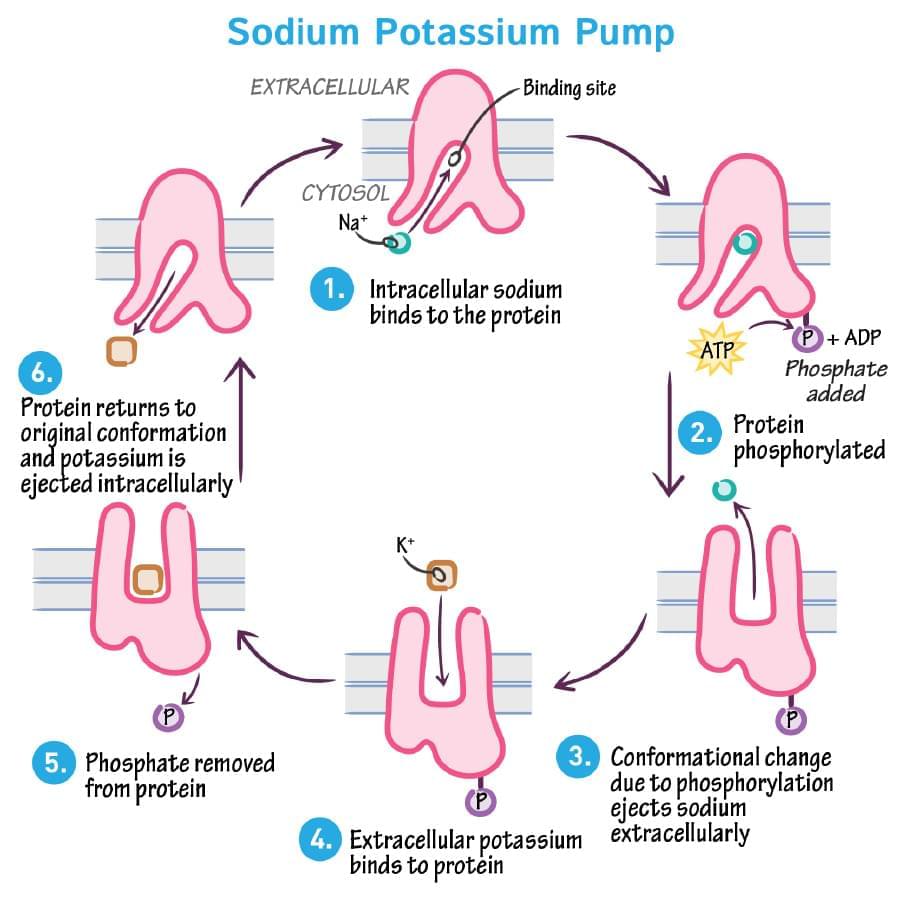
SODIUM/POTASSIUM PUMP • Found in the membrane of all animal cells • Active transport — uses ATP (around 30% of a cell’s total ATP usage) breaking it down to ADP and phosphate • Helps maintain membrane voltage (thought to contribute about 10% of

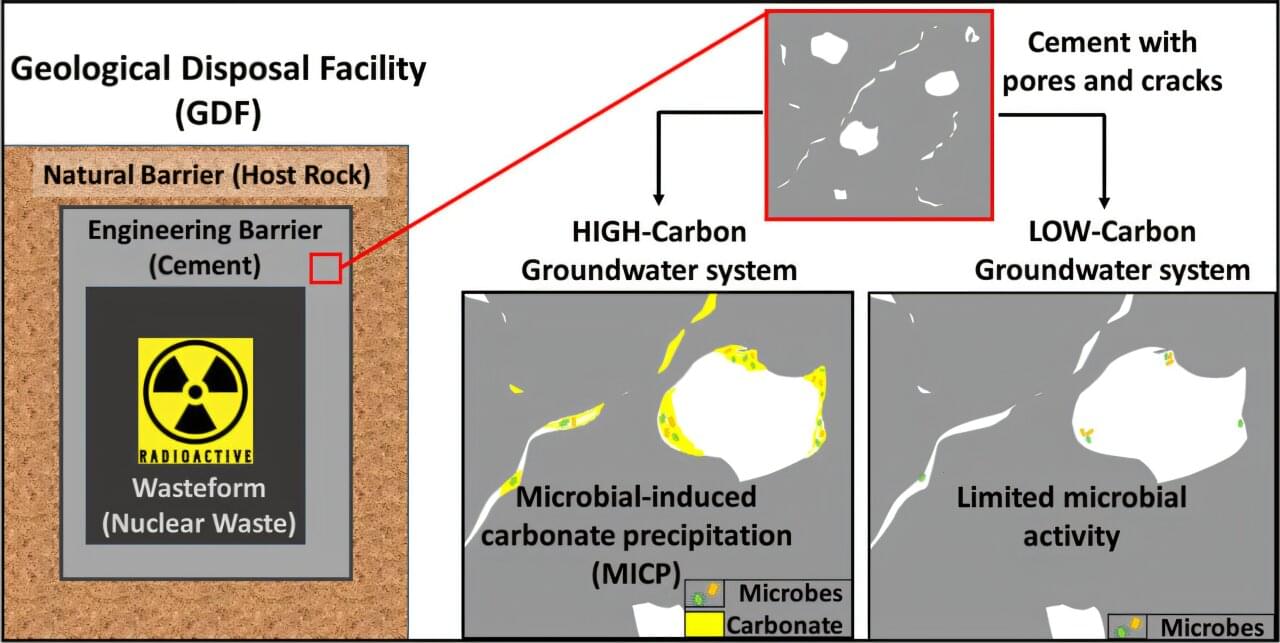
Billions of alkaline-loving microbes could offer a new way to protect nuclear waste buried deep underground. This approach overcomes the limitations of current cement barriers, which can crack or break down over time.
One of the best ways to keep nuclear waste out of harm’s way is to bury it in geological disposal facilities. These are purpose-built containers in tunnels and vaults hundreds of meters underground. Cement is used to provide structural support, seal gaps and encapsulate waste containers. While cement is a strong material, groundwater eventually reacts with it, forming microscopic cracks and pores through which radiation could escape.
This problem is made worse because traditional cement is extremely alkaline (pH greater than 12) and corrosive, which can weaken nearby protective layers such as clay barriers, potentially compromising a facility.
The 6 steps to reach the singularity.
## The technological singularity, a point where AI surpasses human intelligence, is predicted to occur by 2045 and will profoundly transform humanity, requiring proactive adaptation and integration of AI into daily life ## ## Questions to inspire discussion.
Advancing AI and Machine Learning.
🧠 Q: How can we progress towards autonomous machine learning? A: Shift from supervised to unsupervised learning, enabling AI to identify patterns and make predictions without labeled data, thus advancing towards independent learning and improvement.
🤖 Q: What is the significance of achieving Artificial General Intelligence (AGI)? A: AGI represents the pinnacle of AI development, capable of matching or surpassing human-level intelligence across various domains, potentially leading to an unprecedented technological growth boom.
🧬 Q: What are initial steps towards neural augmentation? A: Develop brain-interfacing technologies to enhance specific aspects of human cognition, such as implants or non-invasive devices for improving memory, processing speed, or sensory perception.

Using a tiny, acid-tolerant yeast, scientists have demonstrated a cost-effective way to make disposable diapers, microplastics, and acrylic paint more sustainable through biomanufacturing.
A key ingredient in those everyday products is acrylic acid, an important industrial chemical that gives disposable diapers their absorbency, makes water-based paints and sealants more weather-proof, improves stain resistance in fabric, and enhances fertilizers and soil treatments.
Acrylic acid is converted from a precursor called 3-hydroxypropanoic acid, or 3-HP, which is made almost exclusively from petroleum through chemical synthesis—an energy-intensive process. But 3-HP can also be produced from renewable plant material by using engineered microbes to ferment plant sugars into this high-value chemical. Until now, however, the biomanufacturing process has not proven profitable.
But there is nothing in biology yet found that indicates the inevitability of death. This suggests to me that it is not at all inevitable, and that it is only a matter of time before the biologists discover what it Читать

Inspired by biological systems, materials scientists have long sought to harness self-assembly to build nanomaterials. The challenge: the process seemed random and notoriously difficult to predict.
Now, researchers from the Institute of Science and Technology Austria (ISTA) and Brandeis University have uncovered geometric rules that act as a master control panel for self-assembling particles.
The results, which could find applications ranging from protein design to synthetic nanomachines, were published in Nature Physics.

Celebrating a 7-year anniversary of the first edition of my book The Syntellect Hypothesis (2019)! I can’t help but feel like I’m watching a long-launched probe finally begin to transmit back meaningful data. What started as a speculative framework—half philosophy, half systems theory—has aged into something uncannily timely, as if reality itself had been quietly reading the manuscript and taking notes. In those seven years, AI has gone from clever tool to cognitive co-actor, collective intelligence has accelerated from metaphor to measurable force, and the idea of a convergent, self-reflective Syntellect no longer feels like science fiction so much as a working hypothesis under active experimental validation.
Looking back, the book captured a moment just before the curve went vertical. Looking forward, it reads less like a prediction and more like an early cartography of a terrain we’re now actively inhabiting. The signal is stronger, the noise louder, and the questions sharper—but the core intuition remains intact: intelligence doesn’t merely grow, it integrates. And once it does, history stops being a line and starts behaving more like a phase transition.
Here’s what Google summarizes about the book: The Syntellect Hypothesis: Five Paradigms of the Mind’s Evolution by Alex M. Vikoulov is a book that explores the idea of a future phase transition where human consciousness merges with technology to form a global supermind, or “Syntellect”. It covers topics like digital physics, the technological singularity, consciousness, and the evolution of humanity, proposing that we are on the verge of becoming a single, self-aware superorganism. The book is structured around five paradigms: Noogenesis, Technoculture, the Cybernetic Singularity, Theogenesis, and Universal Mind.
Key Concepts.
Syntellect: A superorganism-level consciousness that emerges when the intellectual synergy of a complex system (like humanity and its technology) reaches a critical threshold. Phase Transition: The book posits that humanity is undergoing a metamorphosis from individual intellect to a collective, higher-order consciousness.
Five Paradigms: The book is divided into five parts that map out this evolutionary journey: Noogenesis: The emergence of mind through computational biology. Technoculture: The rise of human civilization and technology. The Cybernetic Singularity: The point of Syntellect emergence. Theogenesis: Transdimensional propagation and expansion. Universal Mind: The ultimate cosmic level of awareness.
Themes and Scope.
Depression, one of the most prevalent mental health disorders worldwide, is characterized by persistent feelings of sadness, impaired daily functioning and a loss of interest in daily activities, often along with altered sleeping and eating patterns. Past research findings suggest that stress can play a key role in the emergence of depressive symptoms, yet the biological processes via which it might increase the risk of depression remain poorly understood.
Researchers at Wenzhou Medical University, Capital Medical University and other institutes in China recently carried out a study investigating the biological processes that could link stress to the onset of depression. Their results, published in Molecular Psychiatry, suggest that stress influences the levels of a chemical known as formaldehyde (FA) in specific parts of the brain, which could in turn disrupt their normal functioning, contributing to the emergence of depression.

The ability of single active filaments to cluster smaller particles could inspire new materials for building soft robots that perform biological functions.
Every teenager knows that their room will not tidy up by itself. Without intervention, it will inevitably become messier, and they will need to do some work to turn disorder into order. When faced with a similar problem—particle collection—scientists have tried to get individual bacteria, robots, or other self-propelling units to put in the work [1, 2]. But unlike a teenager, a single such unit is usually insufficient to get the job done. Now Rosa Sinaasappel of the University of Amsterdam and her collaborators have proposed and tested a strategy that enables a single active filament to act as a sweeping agent [3]. Thanks to the versatility of polymer architectures, the investigation opens up a huge molecular-design space.
One of life’s most defining properties is its constant struggle against the second law of thermodynamics. At different scales, living organisms need to maintain complex structures or perform directed and persistent motion, feats that would be extraordinarily improbable in thermal equilibrium [4]. Organisms are able to sustain order against entropy by means of constant energy consumption, a feature called “activity.” Conceptually, the sweeping of small objects into piles is a similar problem. The goal is to reach a low-entropy state that is highly disfavored at equilibrium. Bacteria and other active particles, driven by their persistent motion, spontaneously aggregate, and they have been shown to induce clustering of passive particles [1, 2]. However, successful clustering typically requires using a large number of active particles or engineering a complex setting with a favorable geometry [5, 6].
