1. Why Amazon will last longer than most businesses during the Covid-19 epidemic.
2. The challenges Amazon must overcome during the Covid-19 epidemic.
3. Ideas as to how they can overcome the challenge Amazon faces.
Continue reading “Frequently Asked Questions About Novel Coronavirus (COVID-19)” »
“We should plan ahead,” warned physicist Stephen Hawking who died last March, 2018, and was buried next to Isaac Newton. “If a superior alien civilization sent us a text message saying, ‘We’ll arrive in a few decades,’ would we just reply, ‘OK, call us when you get here, we’ll leave the lights on’? Probably not, but this is more or less what has happened with AI.”
The memorial stone placed on top of Hawking’s grave included his most famous equation describing the entropy of a black hole. “Here Lies What Was Mortal Of Stephen Hawking,” read the words on the stone, which included an image of a black hole.
Using algorithms, scientists can simulate how different nanoparticles interact with the antigen component—and how well they activate the immune system.
Researchers at Stanford University have demonstrated they can rejuvenate human cells, making them more like young cells again, by rewinding an epigenetic aging clock.
A gravity laser :DDD.
We consider the possibility of creating a graviton laser. The lasing medium would be a system of contained, ultra cold neutrons. Ultra cold neutrons are a quantum mechanical system that interacts with gravitational fields and with the phonons of the container walls. It is possible to create a population inversion by pumping the system using the phonons. We compute the rate of spontaneous emission of gravitons and the rate of the subsequent stimulated emission of gravitons. The gain obtainable is directly proportional to the density of the lasing medium and the fraction of the population inversion. The applications of a graviton laser would be interesting.
Higgs boson laser.
Electroweak processes in high-energy lepton collisions are considered in a situation where the incident center-of-mass energy lies below the reaction threshold, but is boosted to the required level by subsequent laser acceleration. Within the framework of laser-dressed quantum field theory, we study the laser-boosted process $\ell^+ \ell^- \to HZ^0$ in detail and specify the technical demands needed for its experimental realization. Further, we outline possible qualitative differences to field-free processes regarding the detection of the produced Higgs bosons.
Scientists have accidentally discovered a completely new form of matter that works in the same way as the lightsabers used in Star Wars.
A team of physicists were messing around with photons when they managed to get the particles to stick together and form a molecule.
The molecule behaves, they claim, just like a lightsaber by moving the light particles around in a solid mass and is unlike any matter seen before.
The plaintiffs have sought $20 trillion, which is a bigger amount than China’s GDP, claiming coronavirus is the result of a biological weapon prepared by the Chinese authorities.
They have accused China of aiding and abetting death, provision of material support to terrorists, conspiracy to cause injury and death of US citizens, negligence, wrongful death, and assault and battery.
Also read: Coronavirus impact: India to produce hazmat suits locally as global suppliers say no.
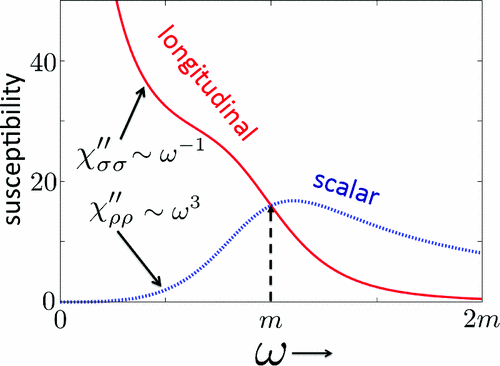
The amplitude mode is a ubiquitous collective excitation in condensed-matter systems with broken continuous symmetry. It is expected in antiferromagnets, short coherence length superconductors, charge density waves, and lattice Bose condensates. Its detection is a valuable test of the corresponding field theory, and its mass gap measures the proximity to a quantum critical point. However, since the amplitude mode can decay into low-energy Goldstone modes, its experimental visibility has been questioned. Here we show that the visibility depends on the symmetry of the measured susceptibility. The longitudinal susceptibility diverges at low frequency as Im χ σ σ ∼ ω − 1 (d = 2) or log (1 / | ω |) (d = 3), which can completely obscure the amplitude peak. In contrast, the scalar susceptibility is suppressed by four extra powers of frequency, exposing the amplitude peak throughout the ordered phase. We discuss experimental setups for measuring the scalar susceptibility. The conductivity of the O (2 ) theory (relativistic superfluid) is a scalar response and therefore exhibits suppressed absorption below the Higgs mass threshold, σ ∼ ω 2 d + 1. In layered, short coherence length superconductors, (relevant, e.g., to cuprates) this threshold is raised by the interlayer plasma frequency.
A gravity laser :DDD.
Higgs boson laser.
