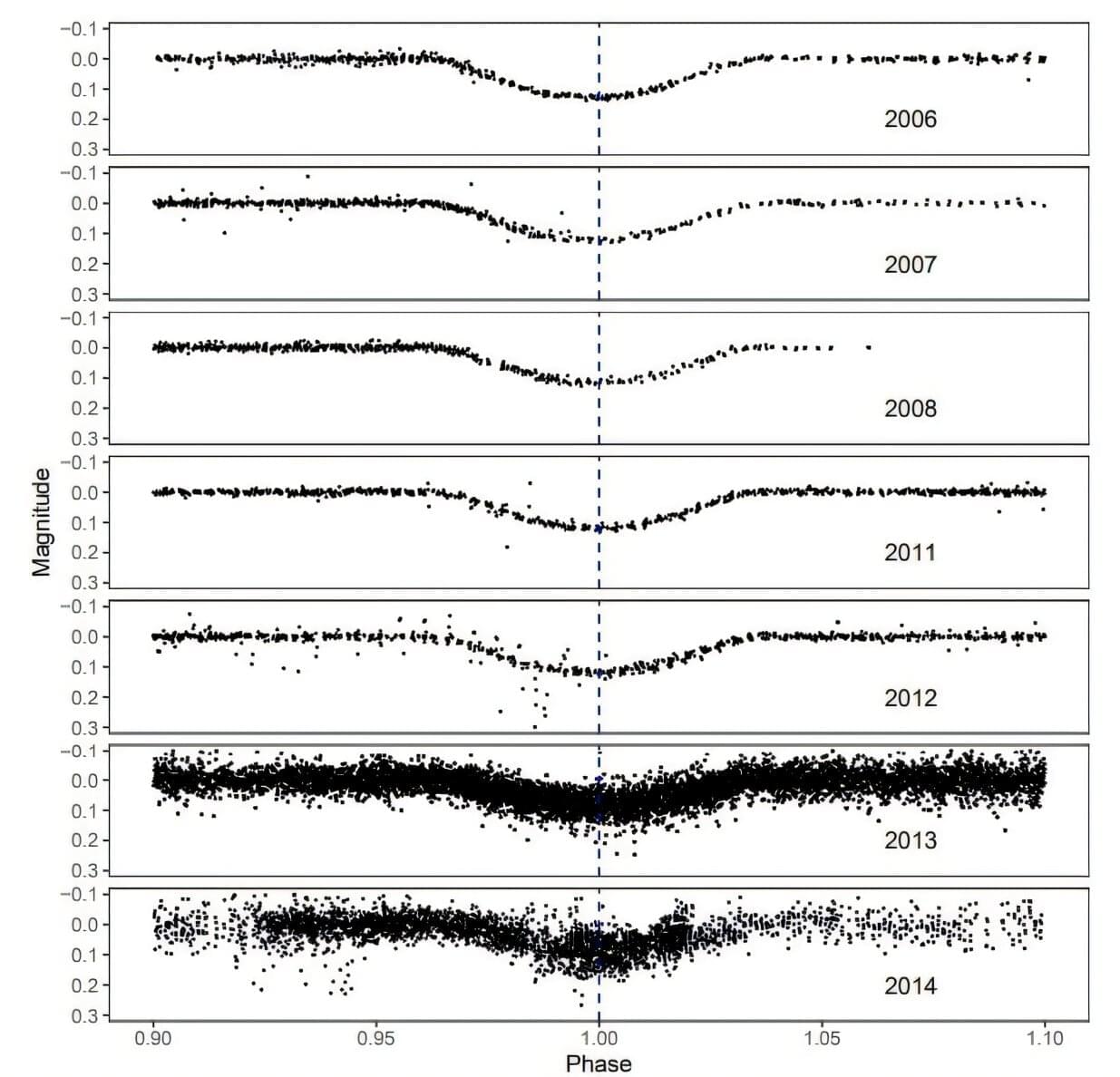
Physicists have long believed that black holes explode at the end of their lives, and that such explosions happen—at most—only once every 100,000 years. But new research published in Physical Review Letters by physicists at the University of Massachusetts Amherst has found a more than 90% probability that one of these black-hole explosions might be seen within the decade, and that, if we are prepared, our current fleet of space and earthbound telescopes could witness the event.
Such an explosion would be strong evidence of a theorized but never observed kind of black hole, called a “primordial black hole,” that could have formed less than a second after the Big Bang occurred, 13.8 billion years ago.
Furthermore, the explosion would give us a definitive catalog of all the subatomic particles in existence, including the ones we have observed, such as electrons, quarks and Higgs bosons, the ones that we have only hypothesized, like dark matter particles, as well as everything else that is, so far, entirely unknown to science. This catalog would finally answer one of humankind’s oldest questions: from where did everything in existence come?