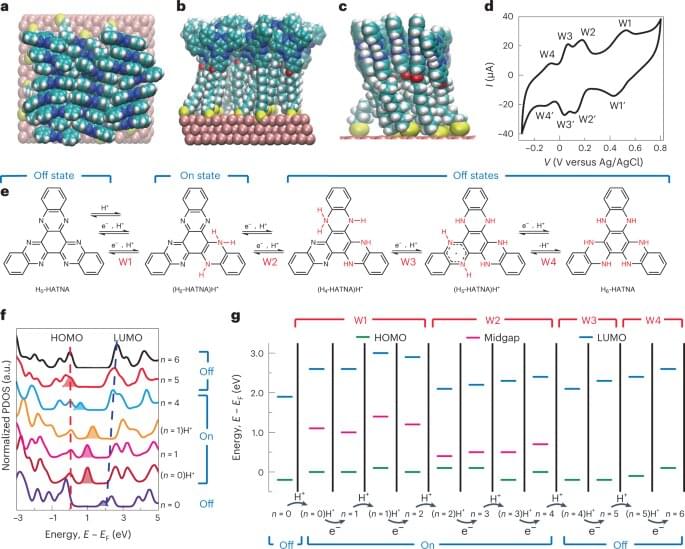
Chemists have created nanorobots propelled by magnets that remove pollutants from water. The invention could be scaled up to provide a sustainable and affordable way of cleaning up contaminated water in treatment plants.
Martin Pumera at the University of Chemistry and Technology, Prague, in the Czech Republic and his colleagues developed the nanorobots by using a temperature-sensitive polymer material and iron oxide. The polymer acts like tiny hands that can pick up and dispose of pollutants in the water, while the iron oxide makes the nanorobots magnetic. The researchers also added oxygen and hydrogen atoms to the iron oxide that can attach onto target pollutants.
The robots are about 200 nanometres wide and are powered by magnetic fields, which allow the team to control their movements.