face_with_colon_three circa 2012.
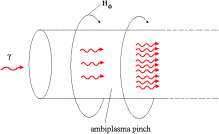
It is shown that the idea of a photon rocket through the complete annihilation of matter with antimatter, first proposed by Sänger, is not a utopian scheme as it is widely believed. Its feasibility appears to be possible by the radiative collapse of a relativistic high current pinch discharge in a hydrogen–antihydrogen ambiplasma down to a radius determined by Heisenberg’s uncertainty principle. Through this collapse to ultrahigh densities the proton–antiproton pairs in the center of the pinch can become the upper gigaelectron volt laser level for the transition into a coherent gamma ray beam by proton–antiproton annihilation, with the magnetic field of the collapsed pinch discharge absorbing the recoil momentum of the beam and transmitting it by the Moessbauer effect to the spacecraft. The gamma ray laser beam is launched as a photon avalanche from one end of the pinch discharge channel. Because of the enormous technical problems to produce and store large amounts of anti-matter, such a propulsion concept may find its first realization in small unmanned space probes to explore nearby solar systems. The laboratory demonstration of a gigaelectron volt gamma ray laser by comparison requiring small amounts of anti-matter may be much closer.