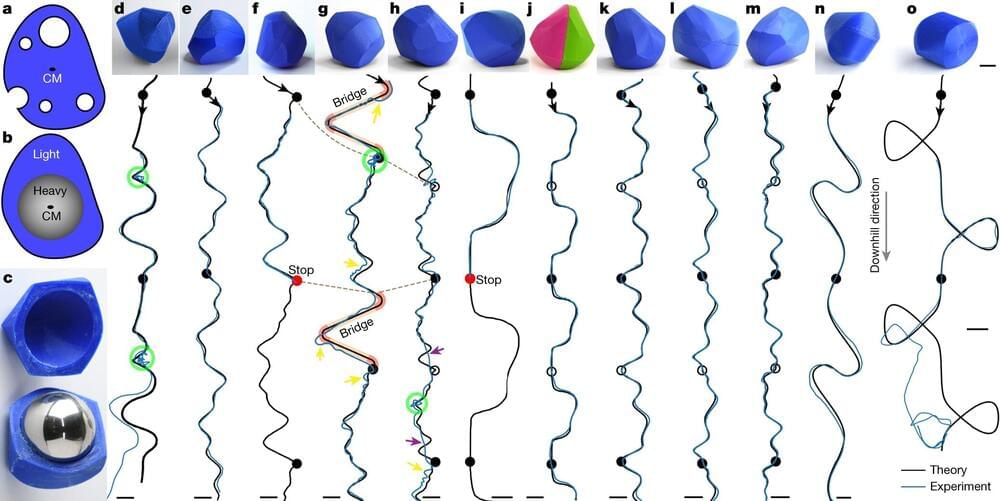
Normally, when we think of a rolling object, we tend to imagine a torus (like a bicycle wheel) or a sphere (like a tennis ball) that will always follow a straight path when rolling. However, the world of mathematics and science is always open to exploring new ideas and concepts. This is why researchers have been studying shapes, like oloids, sphericons and more, which do not roll in straight lines.
All these funky shapes are really interesting to researchers as they can show us new ways to move objects around smoothly and efficiently. For example, imagine reducing the energy required to make a toy robot move, or mixing ingredients more thoroughly with a unique-looking spoon. While these peculiar shapes have been studied before, scientists have now taken it a step further.
Consider a game where you draw a path on a tilted table—similar to tilting a pinball table to make the ball go in a particular direction. Now, try to come up with a 3D object that, when placed at the top of the table, will roll down and exactly follow that path, instead of just going straight down. There are a few other rules of this game: the table needs to be inclined slightly (and not too much), there should be no slipping during rolling, and the initial orientation of the object can be chosen at launch. Plus, the path you draw must never go uphill and must be periodic. It must also consist of identical repeating segments—somewhat like in music rhythm patterns.