A team of researchers around Berlin mathematics professor Michael Joswig is presenting a novel concept for the mathematical modeling of genetic interactions in biological systems. Collaborating with biologists from ETH Zurich and Carnegy Science (U.S.), the team has successfully identified master regulators within the context of an entire genetic network.
The research results provide a coherent theoretical framework for analyzing biological networks and have been published in the Proceedings of the National Academy of Sciences.
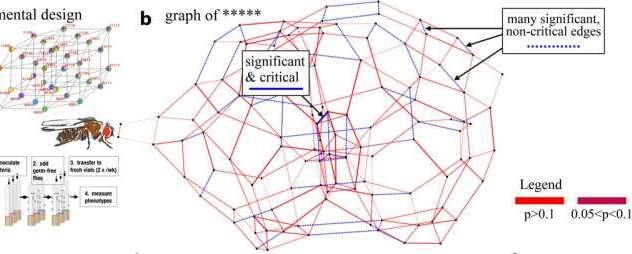
It is a longstanding goal of biologists to determine the key genes and species that have a decisive impact on evolution, ecology, and health. Researchers have now succeeded in identifying certain genes as master regulators in biological networks. These key regulators exert greater control within the system and steer essential cellular processes. Previous studies have mainly focused on pairwise interactions within the system, which can be strongly affected by genetic background or biological context.