Scientists now use a new mathematical model to reveal the geometry of photons, previously elusive.
A groundbreaking study from the University of Birmingham has revealed the shape of a photon and its interaction with quantum emitters.

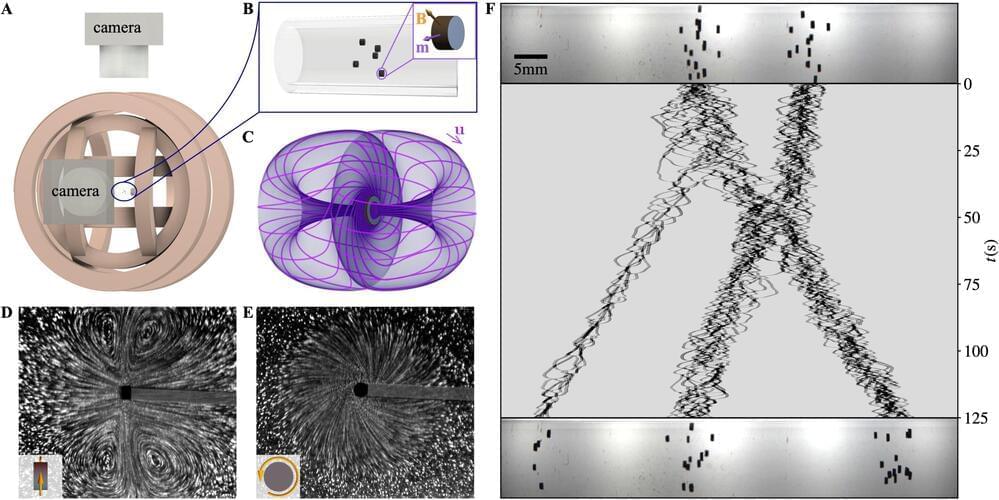
Vorticity, a measure of the local rotation or swirling motion in a fluid, has long been studied by physicists and mathematicians. The dynamics of vorticity is governed by the famed Navier-Stokes equations, which tell us that vorticity is produced by the passage of fluid past walls. Moreover, due to their internal resistance to being sheared, viscous fluids will diffuse the vorticity within them and so any persistent swirling motions will require a constant resupply of vorticity.
Physicists at the University of Chicago and applied mathematicians at the Flatiron Institute recently carried out a study exploring the behavior of viscous fluids in which tiny rotating particles were suspended, acting as local, mobile sources of vorticity. Their paper, published in Nature Physics, outlines fluid behaviors that were never observed before, characterized by self-propulsion, flocking and the emergence of chiral active phases.
“This experiment was a confluence of three curiosities,” William T.M. Irvine, a corresponding author of the paper, told Phys.org. “We had been studying and engineering parity-breaking meta-fluids with fundamentally new properties in 2D and were interested to see how a three-dimensional analog would behave.
Check out courses in science, computer science, or mathematics on Brilliant! First 30 days are free and 20% off the annual premium subscription when you use our link ➜ https://brilliant.org/sabine.
Ten years ago, physicists discovered an anomaly that was dubbed the “ATOMKI anomaly”. The decays of certain atomic nuclei disagreed with our current understanding of physics. Particle physicists assigned the anomaly to a new particle, X17, often described as a fifth force. The anomaly was now tested by a follow-up experiment, but this is only the latest twist in a rather confusing story.
Paper: https://journals.aps.org/prl/abstract…
🤓 Check out my new quiz app ➜ http://quizwithit.com/
💌 Support me on Donorbox ➜ https://donorbox.org/swtg.
📝 Transcripts and written news on Substack ➜ https://sciencewtg.substack.com/
👉 Transcript with links to references on Patreon ➜ / sabine.
📩 Free weekly science newsletter ➜ https://sabinehossenfelder.com/newsle…
👂 Audio only podcast ➜ https://open.spotify.com/show/0MkNfXl…
🔗 Join this channel to get access to perks ➜
/ @sabinehossenfelder.
🖼️ On instagram ➜ / sciencewtg.
#science #sciencenews #physics
To try everything Brilliant has to offer—free—for a full 30 days, visit https://brilliant.org/ArtemKirsanov. You’ll also get 20% off an annual premium subscription.
Socials:
X/Twitter: https://twitter.com/ArtemKRSV
Patreon: / artemkirsanov.
My name is Artem, I’m a graduate student at NYU Center for Neural Science and researcher at Flatiron Institute (Center for Computational Neuroscience).
In this video, we explore the Nobel Prize-winning Hodgkin-Huxley model, the foundational equation of computational neuroscience that reveals how neurons generate electrical signals. We break down the biophysical principles of neural computation, from membrane voltage to ion channels, showing how mathematical equations capture the elegant dance of charged particles that enables information processing.
Outline:
00:00 Introduction.
01:28 Membrane Voltage.
04:56 Action Potential Overview.
6:24 Equilibrium potential and driving force.
10:11 Voltage-dependent conductance.
16:50 Review.
20:09 Limitations \& Outlook.
21:21 Sponsor: Brilliant.org.
22:44 Outro.

Observations of the cosmic microwave background, leftover light from when the Universe was only 380,000 years old, reveal that our cosmos is not rotating. Infinitely long cylinders don’t exist. The interiors of black holes throw up singularities, telling us that the math of GR is breaking down and can’t be trusted. And wormholes? They’re frighteningly unstable. A single photon passing down the throat of a wormhole will cause it to collapse faster than the speed of light. Attempts to stabilize wormholes require exotic matter (as in, matter with negative mass, which isn’t a thing), and so their existence is just as debatable as time travel itself.
This is the point where physicists get antsy. General relativity is telling us exactly where time travel into the past can be allowed. But every single example runs into other issues that have nothing to do with the math of GR. There is no consistency, no coherence among all these smackdowns. It’s just one random rule over here, and another random fact over there, none of them related to either GR or each other.
If the inability to time travel were a fundamental part of our Universe, you’d expect equally fundamental physics behind that rule. Yet every time we discover a CTC in general relativity, we find some reason it’s im possible (or at the very least, implausible), and the reason seems ad hoc. There isn’t anything tying together any of the “no time travel for you” explanations.

Letting AI models communicate with each other in their internal mathematical language, rather than translating back and forth to English, could accelerate their task-solving abilities.
String theory aims to explain all fundamental forces and particles in the universe—essentially, how the world operates on the smallest scales. Though it has not yet been experimentally verified, work in string theory has already led to significant advancements in mathematics and theoretical physics.
Dr. Ksenia Fedosova, a researcher at the Mathematics Münster Cluster of Excellence at the University of Münster has, along with two co-authors, added a new piece to this puzzle: They have proven a conjecture related to so-called 4-graviton scattering, which physicists have proposed for certain equations. The results have been published in the Proceedings of the National Academy of Sciences.
Gravitons are hypothetical particles responsible for gravity. “The 4-graviton scattering can be thought of as two gravitons moving freely through space until they interact in a ‘black box’ and then emerge as two gravitons,” explains Fedosova, providing the physical background for her work. “The goal is to determine the probability of what happens in this black box.”

AI-human collaboration could possibly achieve superhuman greatness in mathematics.
Mathematicians explore ideas by proposing conjectures and proving them with theorems. For centuries, they built these proofs line by careful line, and most math researchers still work like that today. But artificial intelligence is poised to fundamentally change this process. AI assistants nicknamed “co-pilots” are beginning to help mathematicians develop proofs—with a real possibility this will one day let humans answer some problems that are currently beyond our mind’s reach.

The rise of quantum computing is more than a technological advancement; it marks a profound shift in the world of cybersecurity, especially when considering the actions of state-sponsored cyber actors. Quantum technology has the power to upend the very foundations of digital security, promising to dismantle current encryption standards, enhance offensive capabilities, and recalibrate the balance of cyber power globally. As leading nations like China, Russia, and others intensify their investments in quantum research, the potential repercussions for cybersecurity and international relations are becoming alarmingly clear.
Imagine a world where encrypted communications, long thought to be secure, could be broken in mere seconds. Today, encryption standards such as RSA or ECC rely on complex mathematical problems that would take traditional computers thousands of years to solve. Quantum computing, however, changes this equation. Using quantum algorithms like Shor’s, a sufficiently powerful quantum computer could factorize these massive numbers, effectively rendering these encryption methods obsolete.
This capability could give state actors the ability to decrypt communications, access sensitive governmental data, and breach secure systems in real time, transforming cyber espionage. Instead of months spent infiltrating networks and monitoring data flow, quantum computing could provide immediate access to critical information, bypassing traditional defenses entirely.
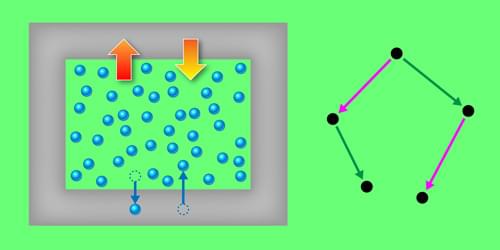
The identification of a new type of symmetry in statistical mechanics could help scientists derive and interpret fundamental relationships in this branch of physics.
Symmetry is a foundational concept in physics, describing properties that remain unchanged under transformations such as rotation and translation. Recognizing these invariances, whether intuitively or through complex mathematics, has been pivotal in developing classical mechanics, the theory of relativity, and quantum mechanics. For example, the celebrated standard model of particle physics is built on such symmetry principles. Now Matthias Schmidt and colleagues at the University of Bayreuth, Germany, have identified a new type of invariance in statistical mechanics (the theoretical framework that connects the collective behavior of particles to their microscopic interactions) [1]. With this discovery, the researchers offer a unifying perspective on subtle relationships between observable properties and provide a general approach for deriving new relations.
The concept of conserved, or time-invariant, properties has roots in ancient philosophy and was crucial to the rise of modern science in the 17th century. Energy conservation became a cornerstone of thermodynamics in the 19th century, when engineers uncovered the link between heat and work. Another important type of invariance is Galilean invariance, which states that the laws of physics are identical in all reference frames moving at a constant velocity relative to each other, resulting in specific relations between positions and velocities in different frames. Its extension, Lorentz invariance, posits that the speed of light is independent of the reference frame. Einstein’s special relativity is based on Lorentz invariance, while his general relativity broadens the idea to all coordinate transformations. These final examples illustrate that invariance not only provides relations between physical observables but can shape our understanding of space, time, and other basic concepts.