Paper: https://arxiv.org/abs/2502.12110v1
GitHub Page: https://github.com/WujiangXu/AgenticMemory
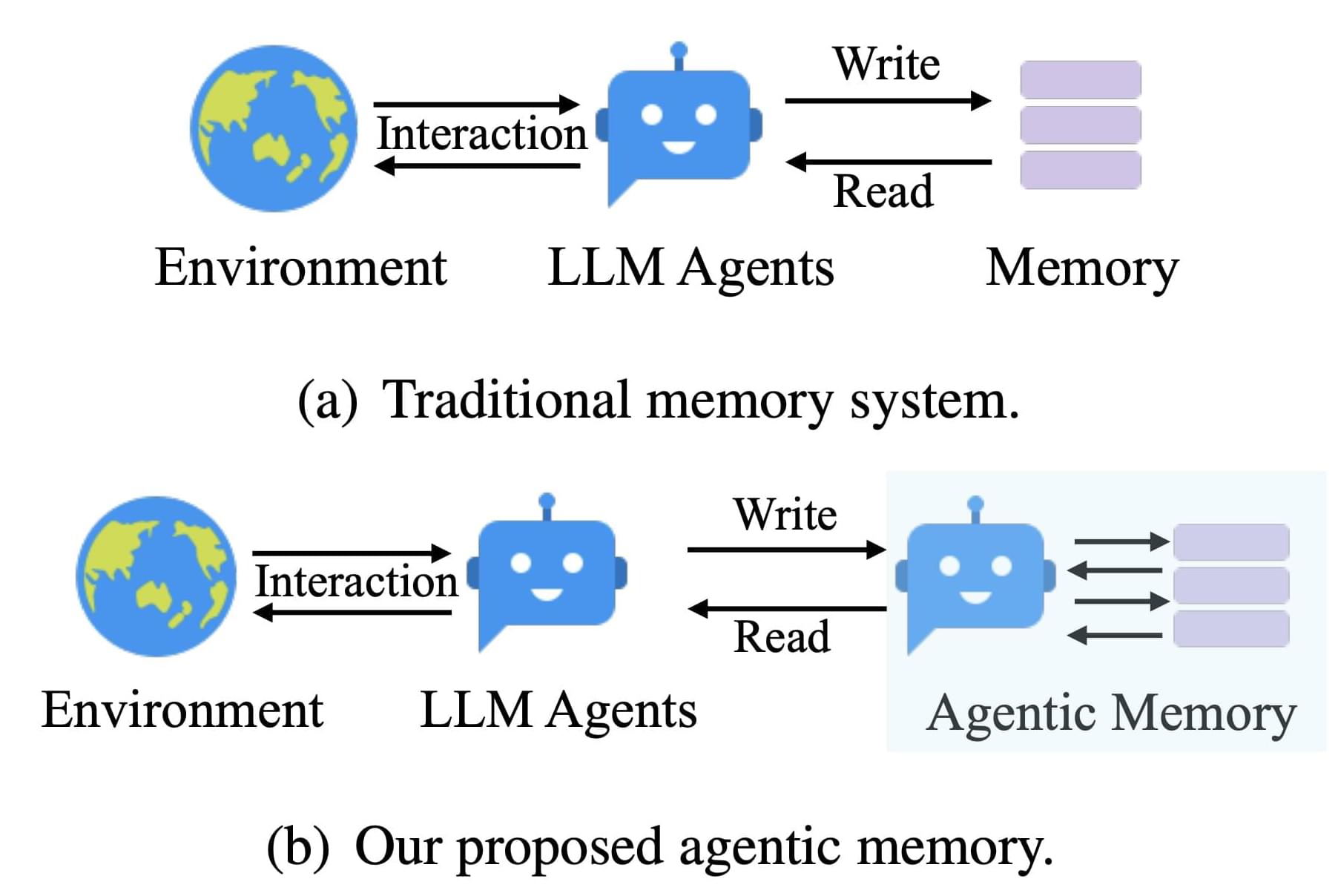
Current memory systems for large language model (LLM) agents often struggle with rigidity and a lack of dynamic organization. Traditional approaches rely on fixed memory structures—predefined storage points and retrieval patterns that do not easily adapt to new or unexpected information. This rigidity can hinder an agent’s ability to effectively process complex tasks or learn from novel experiences, such as encountering a new mathematical solution. In many cases, the memory operates more as a static archive than as a living network of evolving knowledge. This limitation becomes particularly apparent during multi-step reasoning tasks or long-term interactions, where flexible adaptation is crucial for maintaining consistency and depth in understanding.
Researchers from Rutgers University, Ant Group, and Salesforce Research have introduced A-MEM, an agentic memory system designed to address these limitations. A-MEM is built on principles inspired by the Zettelkasten method—a system known for its effective note-taking and flexible organization. In A-MEM, each interaction is recorded as a detailed note that includes not only the content and timestamp, but also keywords, tags, and contextual descriptions generated by the LLM itself. Unlike traditional systems that impose a rigid schema, A-MEM allows these notes to be dynamically interconnected based on semantic relationships, enabling the memory to adapt and evolve as new information is processed.
At its core, A-MEM employs a series of technical innovations that enhance its flexibility. Each new interaction is transformed into an atomic note, enriched with multiple layers of information—keywords, tags, and context—that help capture the essence of the experience. These notes are then converted into dense vector representations using a text encoder, which enables the system to compare new entries with existing memories based on semantic similarity. When a new note is added, the system retrieves similar historical memories and autonomously establishes links between them. This process, which relies on the LLM’s ability to recognize subtle patterns and shared attributes, goes beyond simple matching to create a more nuanced network of related information.