Ever since Archimedes, mathematicians have been fascinated by equations that involve a difference between squares. Now two mathematicians have proven how often these equations have solutions, concluding a decades-old quest.


Agility Robotics recently raised $150 million USD in part from Amazon to further develop its humanoid robot called “Digit” for logistics automation. New wearable, bendable, stretchable neuromorphic AI chip monitors health in real time. New machine learning model from MIT does college level math at a human level.
AI News Timestamps:
0:00 Humanoid Robot Worker For Amazon Automation.
3:00 New Wearable AI Chip.
5:08 New Machine Learning Math Model.
👉 Crypto AI News: https://www.youtube.com/c/CryptoAINews/videos.
#ai #robot #news
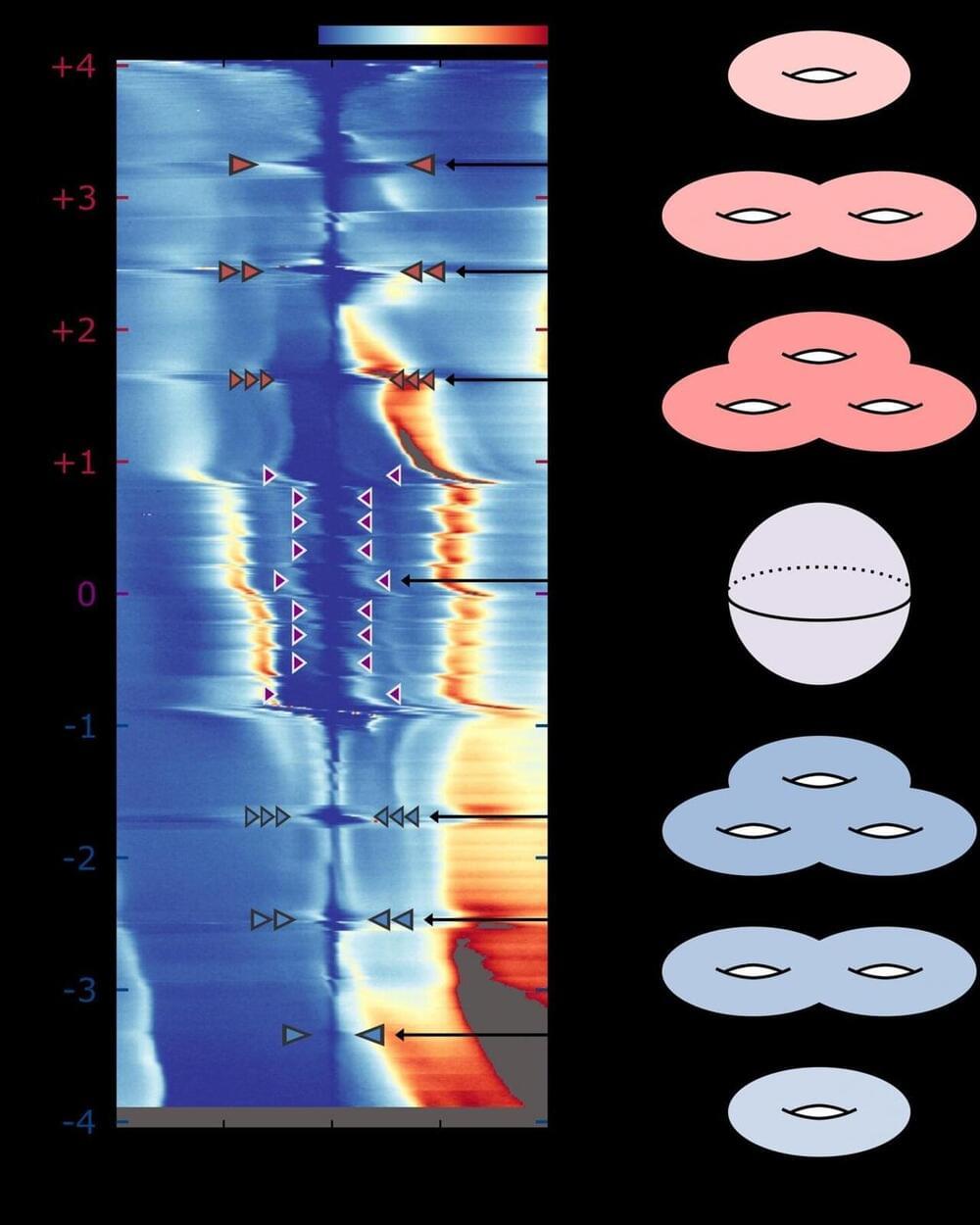
Electrons inhabit a strange and topsy-turvy world. These infinitesimally small particles have never ceased to amaze and mystify despite the more than a century that scientists have studied them. Now, in an even more amazing twist, physicists have discovered that, under certain conditions, interacting electrons can create what are called ‘topological quantum states.’ This finding, which was recently published in the journal Nature, has implications for many technological fields of study, especially information technology.
Topological states of matter are particularly intriguing classes of quantum phenomena. Their study combines quantum physics with topology, which is the branch of theoretical mathematics that studies geometric properties that can be deformed but not intrinsically changed. Topological quantum states first came to the public’s attention in 2016 when three scientists—Princeton’s Duncan Haldane, who is Princeton’s Thomas D. Jones Professor of Mathematical Physics and Sherman Fairchild University Professor of Physics, together with David Thouless and Michael Kosterlitz—were awarded the Nobel Prize for their work in uncovering the role of topology in electronic materials.
“The last decade has seen quite a lot of excitement about new topological quantum states of electrons,” said Ali Yazdani, the Class of 1909 Professor of Physics at Princeton and the senior author of the study. “Most of what we have uncovered in the last decade has been focused on how electrons get these topological properties, without thinking about them interacting with one another.”


Circa 2017
There are many theories about how life evolved on the planet Earth, from formation under a layer of ice, protected from the UV radiation above, to vents in the deep sea that provided hydrogen-rich molecules. But now one team of scientists has found quantitative results that support a theory that is literally out of this world. Organic molecules from meteorites that landed in small, warm pools of water may have delivered the ingredients necessary for life to form on Earth.
The team reached this conclusion through a mathematical model. They took data about planet formation, geology, biology and chemistry and inputted these factors into a grand quantitative model they had designed. Their results support the theory that RNA polymers formed in small, warm ponds of water. Meteorites contributed to this process by transferring enough organic molecules to these pools to ensure that RNA started self-replicating in at least one pool.
What’s more, the team discovered that, according to their calculations, life may have have begun on Earth rather early. The process may have started just a few hundred million years after the planet cooled sufficiently to support liquid surface water. The results were published in Proceedings of the National Academy of Sciences.

Alien communication could utilize quantum physics, so SETI needs a new way to listen.
The Fermi paradox, the “where is everybody?” puzzle, is a persistent question in the search for life in the universe. It asks why, if life is not exceedingly rare in the cosmos, it hasn’t shown up on our doorstep. Equally we might ask why we haven’t even heard from alien life, through radio signals or any other means. A part of the answer could be that our present work on the search for extraterrestrial intelligence is actually very limited. Estimates show that we’ve only examined the equivalent of a hot tub of water compared to all the world’s oceans in our combing through the electromagnetic information that rolls in from the cosmos.1
If you’re a glass-half-full kind of person you’ll see this as an opportunity, but the problem is that we don’t actually know what might be filling the glass in the first place. The vast majority of SETI studies look for structure in electromagnetic radiation, whether in amplitude or frequency modulations of radio waves, or regularity in pulses of light, or in multi-wavelength correlations. In other words, we assume that information might be sailing past us in representations built using classical physics. But what if that’s just wrong?
In recent years a small cadre of physicists and astrophysicists have examined the possibilities for communication across the universe that uses the quantum properties of matter and radiation.2 Here on Earth quantum mechanics is perhaps the greatest triumph and the greatest headache of 20th-century physics. As theories go it has repeatedly validated itself through some of the most exquisite measurements we’ve ever made about the world, yet it remains profoundly challenging because of its counterintuitive rules and contentious interpretations. Even the “simple stuff” is hard, including the basic mathematical tools needed to describe how matter and radiation futz around in weird states of uncertain superposition (think Schrödinger’s cat) or mind-bending entanglement, where properties are linked across space and time, yet never definite until interactions occur.
A new study corrects an important error in the 3D mathematical space developed by the Nobel Prize-winning physicist Erwin Schrödinger and others, and used by scientists and industry for more than 100 years to describe how your eye distinguishes one color from another. The research has the potential to boost scientific data visualizations, improve TVs and recalibrate the textile and paint industries.
“The assumed shape of color space requires a paradigm shift,” said Roxana Bujack, a computer scientist with a background in mathematics who creates scientific visualizations at Los Alamos National Laboratory. Bujack is lead author of the paper by a Los Alamos team in the Proceedings of the National Academy of Sciences on the mathematics of color perception.
“Our research shows that the current mathematical model of how the eye perceives color differences is incorrect. That model was suggested by Bernhard Riemann and developed by Hermann von Helmholtz and Erwin Schrödinger—all giants in mathematics and physics—and proving one of them wrong is pretty much the dream of a scientist,” said Bujack.

Quantum computing will change everything.
“I think I can safely say that nobody really understands quantum mechanics,” renowned physicist Richard Feynman stated once. That shouldn’t come as a big surprise as quantum physics has a reputation for being exceptionally enigmatic. This was the selling point for the quantum physicist Dr. Shohini Ghose from Wilfrid Laurier University.
Having always excelled at mathematics and physics, Ghose was always interested in mysteries, detective stories, and mathematics. This led her to an intense fascination with physics, as she quickly discovered that she could use mathematics to help solve the mysteries of the universe.
Full Story:
IE talked with Shohini Ghose about how quantum computers might transform our future, the mysteries of quantum mechanics, and what the quantum scene will look like in 2027.

Researchers find mathematical trick to combining planetary surface data.
Researchers have discovered a method for making high-resolution maps of planetary surfaces like the moon’s by combining available imagery and topography data.
Mapping the complex and diverse surface of a world like the moon in detailed resolution is challenging because laser altimeters, which measure changes in altitudes, operate at much lower resolution than cameras. And although photographs offer a sense of surface features, it’s difficult to translate images into specific heights and depths.