Researchers identify Brown-Zak fermions in superlattices made from the carbon sheet.

Researchers at the University of Manchester in the UK have identified a new family of quasiparticles in superlattices made from graphene sandwiched between two slabs of boron nitride. The work is important for fundamental studies of condensed-matter physics and could also lead to the development of improved transistors capable of operating at higher frequencies.

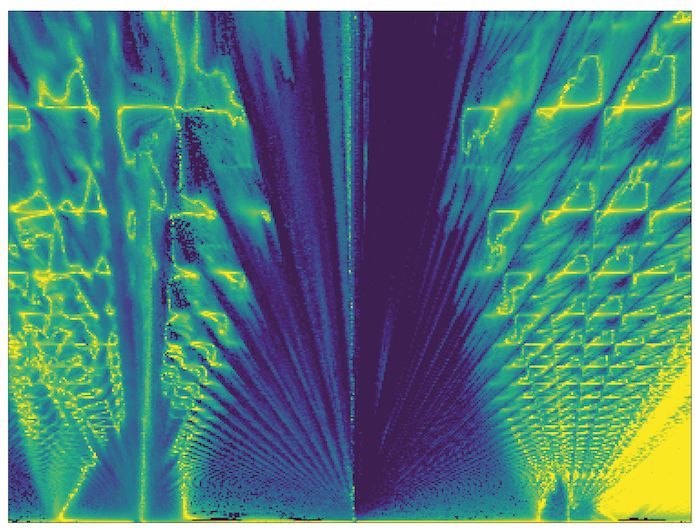
In recent years, physicists and materials scientists have been studying ways to use the weak (van der Waals) coupling between atomically thin layers of different crystals to create new materials in which electronic properties can be manipulated without chemical doping. The most famous example is graphene (a sheet of carbon just one atom thick) encapsulated between another 2D material, hexagonal boron nitride (hBN), which has a similar lattice constant. Since both materials also have similar hexagonal structures, regular moiré patterns (or “superlattices”) form when the two lattices are overlaid.

If the stacked layers of graphene-hBN are then twisted, and the angle between the two materials’ lattices decreases, the size of the superlattice increases. This causes electronic band gaps to develop through the formation of additional Bloch bands in the superlattice’s Brillouin zone (a mathematical construct that describes the fundamental ideas of electronic energy bands). In these Bloch bands, electrons move in a periodic electric potential that matches the lattice and do not interact with one another.