Describes and demonstrates the MR technique of Diffusion Tensor Imaging and reviews some of the basic mathematics of Tensors including matrix multiplication, eigenvalues and eigenvectors.
Category: mathematics – Page 105

Atom: Topological qubits will be one of the key ingredients in the Microsoft plan to bring a powerful, scalable quantum computing solution to the world
Providing increased resistance to outside interference, topological qubits create a more stable foundation than conventional qubits. This increased stability allows the quantum computer to perform computations that can uncover solutions to some of the world’s toughest problems.
While qubits can be developed in a variety of ways, the topological qubit will be the first of its kind, requiring innovative approaches from design through development. Materials containing the properties needed for this new technology cannot be found in nature—they must be created. Microsoft brought together experts from condensed matter physics, mathematics, and materials science to develop a unique approach producing specialized crystals with the properties needed to make the topological qubit a reality.
Exposing the Strange Blueprint Behind “Reality” (Donald Hoffman Interview)
Donald Hoffman interview on spacetime, consciousness, and how biological fitness conceals reality. We discuss Nima Arkani-Hamed’s Amplituhedron, decorated permutations, evolution, and the unlimited intelligence.
The Amplituhedron is a static, monolithic, geometric object with many dimensions. Its volume codes for amplitudes of particle interactions & its structure codes for locality and unitarity. Decorated permutations are the deepest core from which the Amplituhedron gets its structure. There are no dynamics, they are monoliths as in 2001: A Space Odyssey.
Background.
0:00 Highlights.
6:55 The specific limits of evolution by natural selection.
10:50 Don’s born in a San Antonio Army hospital in 1955 (and his parents’ background)
14:44 As a teenager big question he wanted answered, “Are we just machines?“
17:23 Don’s early work as a vision researcher; visual systems construct.
20:43 Carlos’s 3-part series on Fitness-Beats-Truth Theorem.
Fitness-Beats-Truth Theorem.
22:29 Clarifications on FBT: Game theory simulations & math proofs.
24:20 What does he mean I can’t see reality? Fitness payoff functions don’t know about the truth… 28:23 Evolution shapes sensory systems to guide adaptive behavior… consider the virtual reality headset 32:45 FBT doesn’t include costs for extra bits of information processing 34:40 Joscha Bach’s “There are no colors in the universe”… though even light itself isn’t fundamental! 36:36 Map-territory relationship 40:27 Infinite regress, Godel’s Incompleteness Theorem 42:27 Erik Hoel’s causal emergence theory 45:40 Don’s take on causality: there are no causal powers within spacetime What’s Beyond Spacetime? 50:50 Nima Arkani-Hamed’s Amplituhedron 53:00 What percentage of physicists would agree spacetime is doomed? 56:00 Amplituhedron a static, monolithic, geometric object with many dimensions… 59:23 Ties to holographic principle, Ads-CFT correspondence 1:03:13 Quantum error correction 1:05:23 James Gates’ adinkra animations linking electromagnetism & electron-like objects The Unlimited Intelligence 1:08:30 Does Don still meditate 3 hours every day? 1:11:30 “We’re here for the ride…” 1:12:27 All my theories are trivial, there’s an unlimited intelligence that transcends 1:14:00 Carlos meanders on meditation 1:15:50 “You can’t know the truth, but you can be the truth” 1:17:43 Explore-Exploit Tradeoff (foraging strategy) 1:19:15 “You’re absolutely knocking on the right doors here”… our 4D spacetime for some reason essential for consciousness 1:21:10 Why this world, with these symbols, this interface? 1:22:20 “My guess, one of the cheaper headsets” Conscious Realism 1:24:40 Precise, mathematical model of consciousness… the end of Cantor’s infinities 1:28:30 Fusions of Consciousness paper… bridges between interactions of conscious agents/Markovian dynamics → decorated permutations → the Amplituhedron → spacetime 1:35:20 In a meta way, did Don choose the highest fitness path for his career? 1:39:10 “Don’t believe my theory, not the final word” 1:41:00 Where to find more of Don’s work 🚩Links to Donald Hoffman & More 🚩 “Do we see reality as it is?” (Ted Talk 2015) • Do we see reality…
“Symmetry Does Not Entail Veridicality” lecture (Hoffman 2017)
• Don Hoffman — “Sy…

I Think Faster Than Light Travel is Possible. Here’s Why
There are loopholes.
Try out my quantum mechanics course (and many others on math and science) on Brilliant using the link https://brilliant.org/sabine. You can get started for free, and the first 200 will get 20% off the annual premium subscription.
If you’ve been following my channel for a really long time, you might remember that some years ago I made a video about whether faster-than-light travel is possible. I was trying to explain why the arguments saying it’s impossible are inconclusive and we shouldn’t throw out the possibility too quickly, but I’m afraid I didn’t make my case very well. This video is a second attempt. Hopefully this time it’ll come across more clearly!
💌 Support us on Donatebox ➜ https://donorbox.org/swtg.
👉 Transcript and References on Patreon ➜ https://www.patreon.com/Sabine.
📩 Sign up for my weekly science newsletter. It’s free! ➜ https://sabinehossenfelder.com/newsletter/
🔗 Join this channel to get access to perks ➜
https://www.youtube.com/channel/UC1yNl2E66ZzKApQdRuTQ4tw/join.
00:00 Intro.
Room-temperature superfluidity in a polariton condensate Physics
face_with_colon_three year 2017.
First observed in liquid helium below the lambda point, superfluidity manifests itself in a number of fascinating ways. In the superfluid phase, helium can creep up along the walls of a container, boil without bubbles, or even flow without friction around obstacles. As early as 1938, Fritz London suggested a link between superfluidity and Bose–Einstein condensation (BEC)3. Indeed, superfluidity is now known to be related to the finite amount of energy needed to create collective excitations in the quantum liquid4,5,6,7, and the link proposed by London was further evidenced by the observation of superfluidity in ultracold atomic BECs1,8. A quantitative description is given by the Gross–Pitaevskii (GP) equation9,10 (see Methods) and the perturbation theory for elementary excitations developed by Bogoliubov11. First derived for atomic condensates, this theory has since been successfully applied to a variety of systems, and the mathematical framework of the GP equation naturally leads to important analogies between BEC and nonlinear optics12,13,14. Recently, it has been extended to include condensates out of thermal equilibrium, like those composed of interacting photons or bosonic quasiparticles such as microcavity exciton-polaritons and magnons14,15. In particular, for exciton-polaritons, the observation of many-body effects related to condensation and superfluidity such as the excitation of quantized vortices, the formation of metastable currents and the suppression of scattering from potential barriers2,16,17,18,19,20 have shown the rich phenomenology that exists within non-equilibrium condensates. Polaritons are confined to two dimensions and the reduced dimensionality introduces an additional element of interest for the topological ordering mechanism leading to condensation, as recently evidenced in ref. 21. However, until now, such phenomena have mainly been observed in microcavities embedding quantum wells of III–V or II–VI semiconductors. As a result, experiments must be performed at low temperatures (below ∼ 20 K), beyond which excitons autoionize. This is a consequence of the low binding energy typical of Wannier–Mott excitons. Frenkel excitons, which are characteristic of organic semiconductors, possess large binding energies that readily allow for strong light–matter coupling and the formation of polaritons at room temperature. Remarkably, in spite of weaker interactions as compared to inorganic polaritons22, condensation and the spontaneous formation of vortices have also been observed in organic microcavities23,24,25. However, the small polariton–polariton interaction constants, structural inhomogeneity and short lifetimes in these structures have until now prevented the observation of behaviour directly related to the quantum fluid dynamics (such as superfluidity). In this work, we show that superfluidity can indeed be achieved at room temperature and this is, in part, a result of the much larger polariton densities attainable in organic microcavities, which compensate for their weaker nonlinearities.
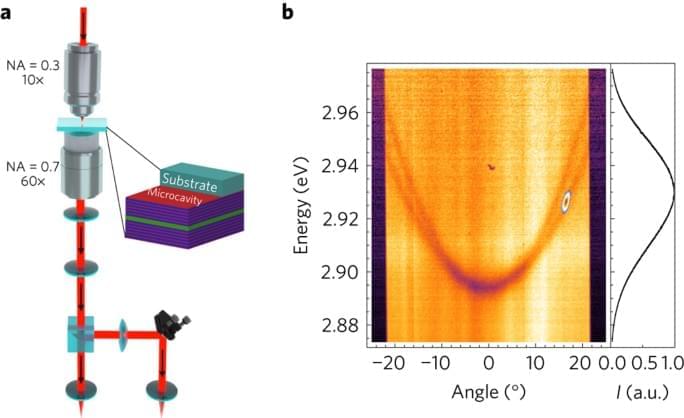
Our sample consists of an optical microcavity composed of two dielectric mirrors surrounding a thin film of 2,7-Bis[9,9-di(4-methylphenyl)-fluoren-2-yl]-9,9-di(4-methylphenyl)fluorene (TDAF) organic molecules. Light–matter interaction in this system is so strong that it leads to the formation of hybrid light–matter modes (polaritons), with a Rabi energy 2 ΩR ∼ 0.6 eV. A similar structure has been used previously to demonstrate polariton condensation under high-energy non-resonant excitation24. Upon resonant excitation, it allows for the injection and flow of polaritons with a well-defined density, polarization and group velocity.
The experimental configuration is shown in Fig. 1a. The sample is positioned between two microscope objectives to allow for measurements in a transmission geometry while maintaining high spatial resolution. A polariton wavepacket with a chosen wavevector is created by exciting the sample with a linearly polarized 35 fs laser pulse resonant with the lower polariton branch (see Methods). By detecting the reflected or transmitted light using a spectrometer and a charge-coupled device (CCD) camera, energy-resolved space and momentum maps can be acquired. An example of the experimental polariton dispersion under white light illumination is shown in Fig. 1b. The parabolic TE-and TM-polarized lower polariton branches appear as dips in the reflectance spectra. The figure also shows an example of how the laser energy, momentum and polarization can be precisely tuned to excite, in this case, the TE lower polariton branch at a given angle.

‘Alien Calculus’ Could Save Particle Physics From Infinities
In the math of particle physics, every calculation should result in infinity. Physicists get around this by just ignoring certain parts of the equations — an approach that provides approximate answers. But by using the techniques known as “resurgence,” researchers hope to end the infinities and end up with perfectly precise predictions.
Neural manifolds — The Geometry of Behaviour
This video is my take on 3B1B’s Summer of Math Exposition (SoME) competition.
It explains in pretty intuitive terms how ideas from topology (or “rubber geometry”) can be used in neuroscience, to help us understand the way information is embedded in high-dimensional representations inside neural circuits.
OUTLINE:
00:00 Introduction.
01:34 — Brief neuroscience background.
06:23 — Topology and the notion of a manifold.
11:48 — Dimension of a manifold.
15:06 — Number of holes (genus)
18:49 — Putting it all together.
____________
Main paper:
Chaudhuri, R., Gerçek, B., Pandey, B., Peyrache, A. & Fiete, I. The intrinsic attractor manifold and population dynamics of a canonical cognitive circuit across waking and sleep. Nat Neurosci 22, 1512–1520 (2019).
_________________________
Other relevant references:
1. Jazayeri, M. & Ostojic, S. Interpreting neural computations by examining intrinsic and embedding dimensionality of neural activity. arXiv:2107.04084 [q-bio] (2021).
2. Gallego, J. A., Perich, M. G., Chowdhury, R. H., Solla, S. A. & Miller, L. E. Long-term stability of cortical population dynamics underlying consistent behavior. Nat Neurosci 23260–270 (2020).
3. Bernardi, S. et al. The Geometry of Abstraction in the Hippocampus and Prefrontal Cortex. Cell 183954–967.e21 (2020).
4. Shine, J. M. et al. Human cognition involves the dynamic integration of neural activity and neuromodulatory systems. Nat Neurosci 22289–296 (2019).
5. Remington, E. D., Narain, D., Hosseini, E. A. & Jazayeri, M. Flexible Sensorimotor Computations through Rapid Reconfiguration of Cortical Dynamics. Neuron 98, 1005–1019.e5 (2018).
6. Low, R. J., Lewallen, S., Aronov, D., Nevers, R. & Tank, D. W. Probing variability in a cognitive map using manifold inference from neural dynamics. http://biorxiv.org/lookup/doi/10.1101/418939 (2018) doi:10.1101/418939.
7. Elsayed, G. F., Lara, A. H., Kaufman, M. T., Churchland, M. M. & Cunningham, J. P. Reorganization between preparatory and movement population responses in motor cortex. Nat Commun 7, 13239 (2016).
8. Peyrache, A., Lacroix, M. M., Petersen, P. C. & Buzsáki, G. Internally organized mechanisms of the head direction sense. Nat Neurosci 18569–575 (2015).
9. Dabaghian, Y., Mémoli, F., Frank, L. & Carlsson, G. A Topological Paradigm for Hippocampal Spatial Map Formation Using Persistent Homology. PLoS Comput Biol 8, e1002581 (2012).
10. Yu, B. M. et al. Gaussian-Process Factor Analysis for Low-Dimensional Single-Trial Analysis of Neural Population Activity. Journal of Neurophysiology 102614–635 (2009).
11. Singh, G. et al. Topological analysis of population activity in visual cortex. Journal of Vision 8, 11–11 (2008).
The majority of animations in this video were made using Manim — an open source python library (github.com/ManimCommunity/manim) and brainrender (github.com/brainglobe/brainrender)