Illuminating mathematics, physics, biology and computer science research through public service journalism.



AInstein robot can respond to inquiries from pupils and even illustrate Albert Einstein’s theory of temporal relativity using a pendulum.
High school students in Cyprus have developed an artificial intelligence (AI) robot that uses ChatGPT to enhance classroom learning.
The Three PASCAL schools’ creation, AInstein, can hold dialogues, produce textual content, and crack jokes, according to an article published on Thursday by Voice of America (VOA).
Fascinating proposal for methodology.
Models are scientific models, theories, hypotheses, formulas, equations, naïve models based on personal experiences, superstitions (!), and traditional computer programs. In a Reductionist paradigm, these Models are created by humans, ostensibly by scientists, and are then used, ostensibly by engineers, to solve real-world problems. Model creation and Model use both require that these humans Understand the problem domain, the problem at hand, the previously known shared Models available, and how to design and use Models. A Ph.D. degree could be seen as a formal license to create new Models[2]. Mathematics can be seen as a discipline for Model manipulation.
But now — by avoiding the use of human made Models and switching to Holistic Methods — data scientists, programmers, and others do not themselves have to Understand the problems they are given. They are no longer asked to provide a computer program or to otherwise solve a problem in a traditional Reductionist or scientific way. Holistic Systems like DNNs can provide solutions to many problems by first learning about the domain from data and solved examples, and then, in production, to match new situations to this gathered experience. These matches are guesses, but with sufficient learning the results can be highly reliable.
We will initially use computer-based Holistic Methods to solve individual and specific problems, such as self-driving cars. Over time, increasing numbers of Artificial Understanders will be able to provide immediate answers — guesses — to wider and wider ranges of problems. We can expect to see cellphone apps with such good command of language that it feels like talking to a competent co-worker. Voice will become the preferred way to interact with our personal AIs.

A synthetic analog of a black hole could tell us a thing or two about an elusive radiation theoretically emitted by the real thing.
Using a chain of atoms in single-file to simulate the event horizon of a black hole, a team of physicists observed the equivalent of what we call Hawking radiation – particles born from disturbances in the quantum fluctuations caused by the black hole’s break in spacetime.
This, they say, could help resolve the tension between two currently irreconcilable frameworks for describing the Universe: the general theory of relativity, which describes the behavior of gravity as a continuous field known as spacetime; and quantum mechanics, which describes the behavior of discrete particles using the mathematics of probability.
Large language models are drafting screenplays and writing code and cracking jokes. Image generators, such as Midjourney and DALL-E 2, are winning art prizes and democratizing interior design and producing dangerously convincing fabrications. They feel like magic. Meanwhile, the world’s most advanced robots are still struggling to open different kinds of doors. As in actual, physical doors. Chatbots, in the proper context, can be—and have been—mistaken for actual human beings; the most advanced robots still look more like mechanical arms appended to rolling tables. For now, at least, our dystopian near future looks a lot more like Her than M3GAN.
The counterintuitive notion that it’s harder to build artificial bodies than artificial minds is not a new one. In 1988, the computer scientist Hans Moravec observed that computers already excelled at tasks that humans tended to think of as complicated or difficult (math, chess, IQ tests) but were unable to match “the skills of a one-year-old when it comes to perception and mobility.” Six years later, the cognitive psychologist Steven Pinker offered a pithier formulation: “The main lesson of thirty-five years of AI research,” he wrote, “is that the hard problems are easy and the easy problems are hard.” This lesson is now known as “Moravec’s paradox.”
An artificial black hole produced using sound waves and a dielectric medium has been created in the lab, according to researchers with an international think tank featuring more than 30 Ph.D. research scientists from around the world.
The researchers say their discovery is significantly more cost-effective and efficient than current methods in use by researchers who want to simulate the effects of a black hole in a laboratory environment.
New York-based Applied Physics first achieved recognition with the 2021 publication of a peer-reviewed theoretical paper detailing the mathematics behind the construction of a physical warp drive. More recently, the organization published a method for using Cal Tech’s Laser Interferometer Gravitational-Wave Observatory (LIGO) to detect the use of warp drives in outer space, co-authored by Dr. Manfred Paulini, the Associate Dean of Physics at Carnegie Mellon University.
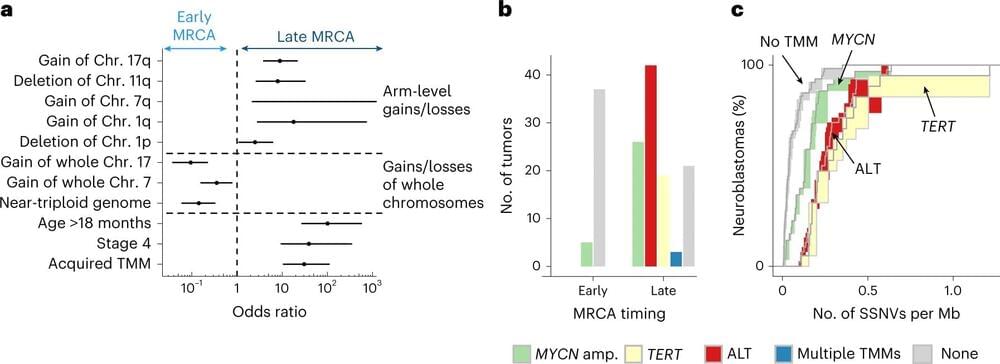
A research team led by the German Cancer Research Center in Heidelberg, Germany, has discovered that the genetic sequence of a tumor can be read like a molecular clock, traced back to its most recent common ancestor cell. Extracting the duration of tumor evolution can give an accurate predictor of neuroblastoma outcomes.
In a paper published in Nature Genetics titled “Neuroblastoma arises in early fetal development and its evolutionary duration predicts outcome,” the team details the steps they took in identifying a genomic clock tested against a whole genome sequenced population combined with analysis and mathematical modeling, to identify evolution markers, traceability and a likely origin point of infant neuroblastomas.
Cancer cells start out life as heroic healthy tissues, with the sort of all for one, one for all, throw yourself on a grenade to save your mates–type attitude that is taking place throughout the body every day. At some point, something goes wrong, and a good cell goes bad.
10 SpaceX Starships are carrying 120 robots to Mars. They are the first to colonize the Red Planet. Building robot habitats to protect themselves, and then landing pads, structures, and the life support systems for the humans who will soon arrive.
This Mars colonization mini documentary also covers they type of robots that will be building on Mars, the solar fields, how Elon Musk and Tesla could have a battery bank station at the Mars colony, and how the Martian colony expands during the 2 years when the robots are building. Known as the Robotic Age of Mars.
Additional footage from: SpaceX, NASA/JPL/University of Arizona, ICON, HASSEL, Tesla, Lockhead Martin.
A building on Mars sci-fi documentary, and a timelapse look into the future.
See more of Venture City at my website: https://vx-c.com.
_______
Books.
• The Martian book showcases the science, math, and physics of living on the red planet — told through the story of someone who has to survive there.
Echopraxia is a book set in one of the most interesting sci-fi universes that I have covered on this channel. It is technically a sequel to Blindsight, but it is not necessary that you read Blindsight to understand Echopraxia is set in the late 21 century. About 14 years after man’s first contact with alien life.
This book brings up one of the most interesting concepts I’ve ever encountered in any sci-fi book ever. And that is the concept of the “Digital Universe” and God as a Virus. Now this is a concept that comes from the field of digital physics, which keep in mind is all theoretical. It is based on the premise that the universe is pure mathematics at its base, every event that occurs can be thought of as a kind of computation. This could mean that the universe is a simulation, but that is not necessary for the idea to work.
The universe could itself be a giant computer, physics would be its software and matter, its hardware. Every movement of an electron would be a calculation in that vast supercomputer. In some models of the Digital Universe, matter itself is merely an instantiation of numbers.
Get Echopraxia: https://www.amazon.com/Echopraxia-Firefall-Book-Peter-Watts-…sr=8-1
Get blindsight: https://www.amazon.com/Blindsight-Peter-Watts-audiobook/dp/B…sr=8-1
My other videos on this series: https://www.youtube.com/playlist?list=PLRXGGVBzHLUcF9_xuNSF8c-NPM29qXxSj.
Art: https://docs.google.com/document/d/1f09FgJsBbvvS1AYIp19fplHG…p=sharing.

The story of modern physics has been one of reductionism. We do not need a vast encyclopedia to understand the inner workings of Nature. Rather, we can describe a near-limitless range of natural phenomena, from the interior of a proton to the creation of galaxies, with apparently unreasonable efficiency using the language of mathematics. In the words of theoretical physicist Eugene Wigner, ‘The miracle of the appropriateness of the language of mathematics for the formulation of the laws of physics is a wonderful gift which we neither understand nor deserve. We should be grateful for it.’
The mathematics of the twentieth century described a Universe populated by a limited number of different types of fundamental particles interacting with each other in an arena known as spacetime according to a collection of rules that can be written down on the back of an envelope. If the Universe was designed, it seemed, the designer was a mathematician.
Today, the study of black holes appears to be edging us in a new direction, towards a language more often used by quantum computer scientists. The language of information. Space and time may be emergent entities that do not exist in the deepest description of Nature. Instead, they are synthesized out of entangled quantum bits of information in a way that resembles a cleverly constructed computer code. If the Universe is designed, it seems, the designer is a programmer.