The world’s leading mathematicians were stunned by how adept artificial intelligence is at doing their jobs.



Since its development 100 years ago, quantum mechanics has revolutionized our understanding of nature, revealing a bizarre world in which an object can act like both waves and particles, and behave differently depending on whether it is being watched.
In recent decades, researchers exploring this wave-particle duality have learned to measure the relative “wave-ness” and “particle-ness” of quantum objects, helping to explain how and when they veer between wave-like or particle-like behaviors.
Now, in a paper for Physical Review Research, researchers at the Stevens Institute of Technology report an important new breakthrough: a simple but powerful formula that describes the precise closed mathematical relationship between a quantum object’s “wave-ness” and “particle-ness.”
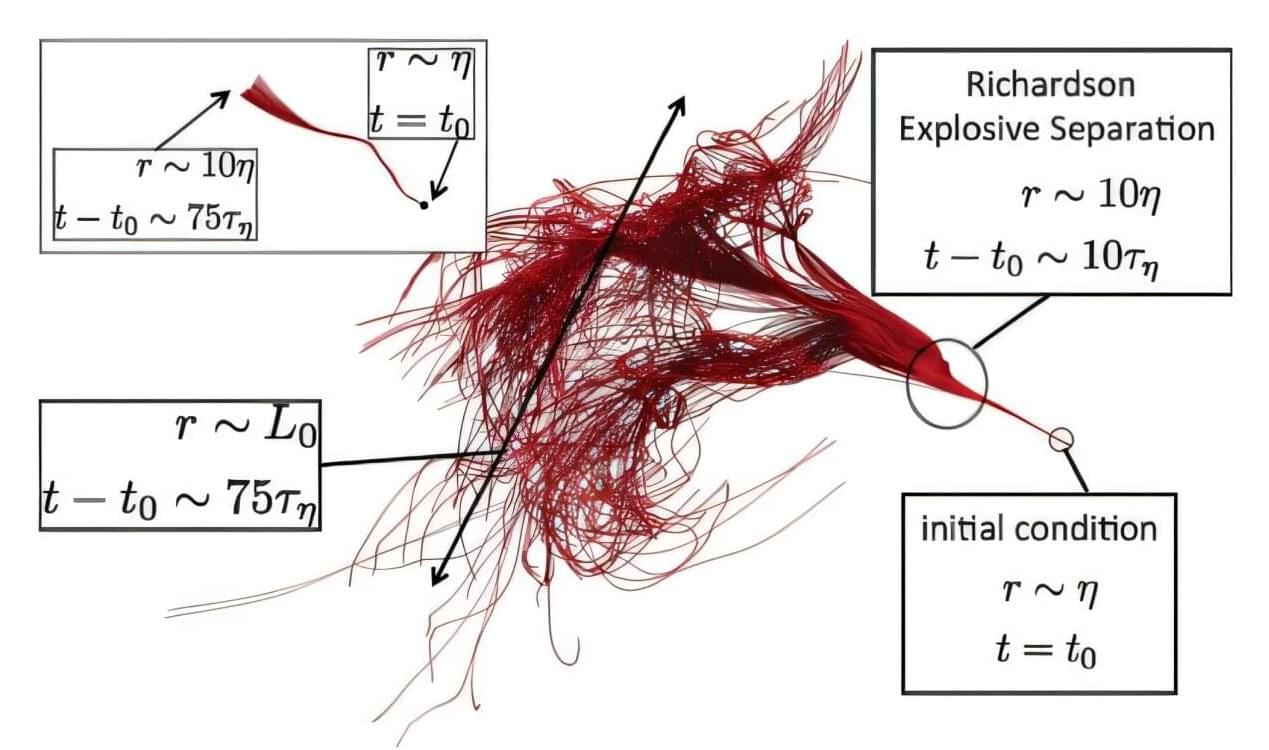
A sneeze. Ocean currents. Smoke. What do these have in common? They’re instances of turbulence: unpredictable, chaotic, uneven fluid flows of fluctuating velocity and pressure. Though ubiquitous in nature, these flows remain somewhat of a mystery, theoretically and computationally.
“Most flows that we encounter in nature are turbulent—it does not matter whether it is the flow outside the airplane that makes us fasten our seatbelts, or the flow in a small stream,” said UC Santa Barbara mathematics professor Björn Birnir.
“Turbulence is difficult to understand because the mathematical models that describe it are nonlinear, stochastic and the solutions are unstable. This made it necessary to develop new theories to truly understand the nature of turbulence.”
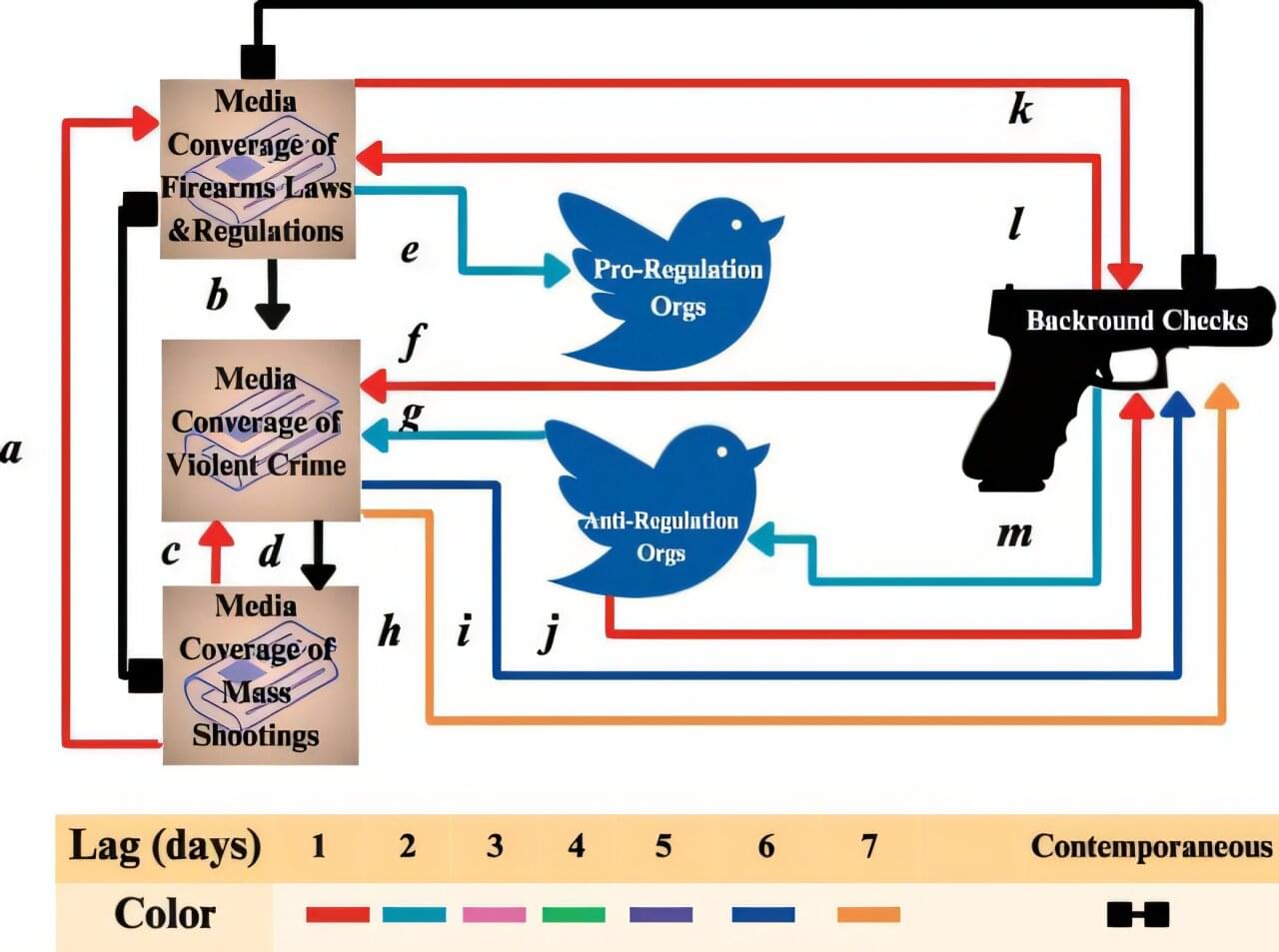
As gun sales in the United States continue to soar, researchers at Georgia State University have uncovered insights into what drives Americans to buy firearms. A new study published in PNAS Nexus journal reveals the complex interaction among media coverage, social media activity and firearm purchases.
Led by Igor Belykh, a Distinguished University Professor of Applied Mathematics at Georgia State, the research team—including Kevin Slote, a Ph.D. student in Georgia State’s mathematics and statistics doctoral program; Kevin Daley, a recent graduate; and co-authors from New York University (NYU) and the New Jersey Institute of Technology (NJIT)—analyzed daily data from 2012 to 2020. Their study explores how gun-rights organizations and regulation advocates influence short-term firearm purchases through social media activity and media coverage.
The study found that social media activity by both sides directly affects gun buying behavior, often triggering purchases within days of posts. Media coverage of violent crime also plays a role, as it spurs discussions among these organizations, further influencing public sentiment toward gun ownership.
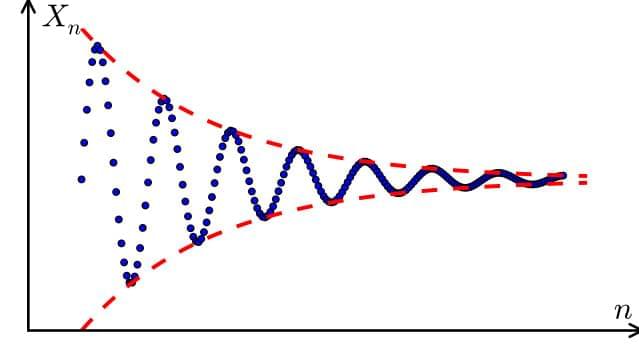
In mathematics, a Cauchy sequence is a sequence whose elements become arbitrarily close to each other as the sequence progresses. [ 1 ] More precisely, given any small positive distance, all excluding a finite number of elements of the sequence are less than that given distance from each other. Cauchy sequences are named after Augustin-Louis Cauchy; they may occasionally be known as fundamental sequences. [ 2 ].

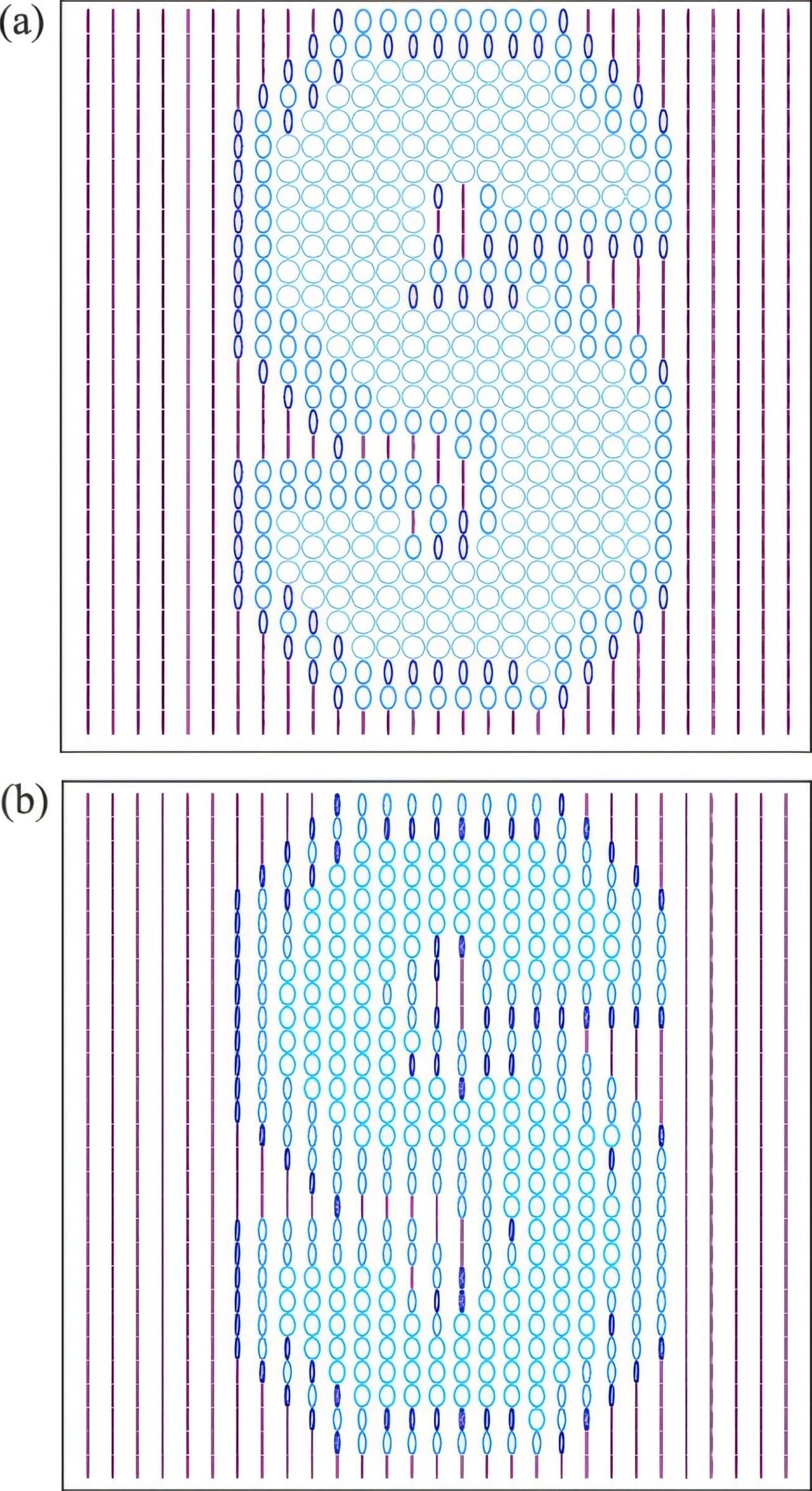
Caltech scientists have found a fast and efficient way to add up large numbers of Feynman diagrams, the simple drawings physicists use to represent particle interactions. The new method has already enabled the researchers to solve a longstanding problem in the materials science and physics worlds known as the polaron problem, giving scientists and engineers a way to predict how electrons will flow in certain materials, both conventional and quantum.
In the 1940s, physicist Richard Feynman first proposed a way to represent the various interactions that take place between electrons, photons, and other fundamental particles using 2D drawings that involve straight and wavy lines intersecting at vertices. Though they look simple, these Feynman diagrams allow scientists to calculate the probability that a particular collision, or scattering, will take place between particles.
Since particles can interact in many ways, many different diagrams are needed to depict every possible interaction. And each diagram represents a mathematical expression. Therefore, by summing all the possible diagrams, scientists can arrive at quantitative values related to particular interactions and scattering probabilities.

Comparing our findings across species with those across growth led us to a final question. If the purpose of sleep shifts from being about neural reorganisation as children to being about repair once we’re grown, when exactly does that transition occur, and how sudden is it? Armed with our new theory plus human developmental data, we could answer this question with surprising accuracy: the transition occurs when we’re extremely young – at about 2.5 years of age – and it happens extremely abruptly, like water freezing at 0°C.
We were delighted with this stunning result. First, it gave us an even greater appreciation for the critical importance of sleep: never again would we underestimate its importance for our children, especially in their first few years of life when their sleep is doing something so fundamentally different and extraordinarily important, something that seemingly can’t be made up for later in life. Second, we had discovered that these two states of sleep, while they looked remarkably similar from the outside, are actually analogous to completely different states of matter before and after the stark dividing line of 2.5 years of age. Before 2.5 years, our brains are more fluid and plastic, enabling us to learn and adapt quickly, similar to the state of water flowing around obstacles. After 2.5 years, our brains are much more crystalline and frozen, still capable of learning and adapting but more like glaciers slowly pushing across a landscape.
Many questions still remain. How much does sleep vary across humans and across species? Can this early fluid phase of sleep be extended? Is this phase already extended or shortened in some individuals, and what costs or benefits are associated with that? What other functions of sleep have piggybacked on to the primary functions of repair and neural reorganisation? How do the different reasons for sleep compete for or share sleep time, either across ages or even within a single night? It will take much more work to fully unravel the mysteries of sleep, but our recent insights – about age-based shifts in the purpose of sleep and the mathematical, predictive theories that quantify them – represent an essential tool to plumb these depths even further.

For decades, scientists have looked to light as a way to speed up computing. Photonic neural networks—systems that use light instead of electricity to process information—promise faster speeds and lower energy use than traditional electronics.
But despite their potential, these systems have struggled to match the accuracy of digital neural networks. A key reason: most photonic systems still mimic the structure and training methods of digital models, introducing errors when translating from software to hardware.
Now, a research team from Northwestern Polytechnical University and Southeast University in China has developed a new kind of photonic neural network that breaks free from this digital imitation. Their design, published in Advanced Photonics Nexus, uses physical transformations of light to process information directly, without relying on mathematical models. This approach not only improves accuracy but also highlights a new direction for building smarter, faster AI hardware.
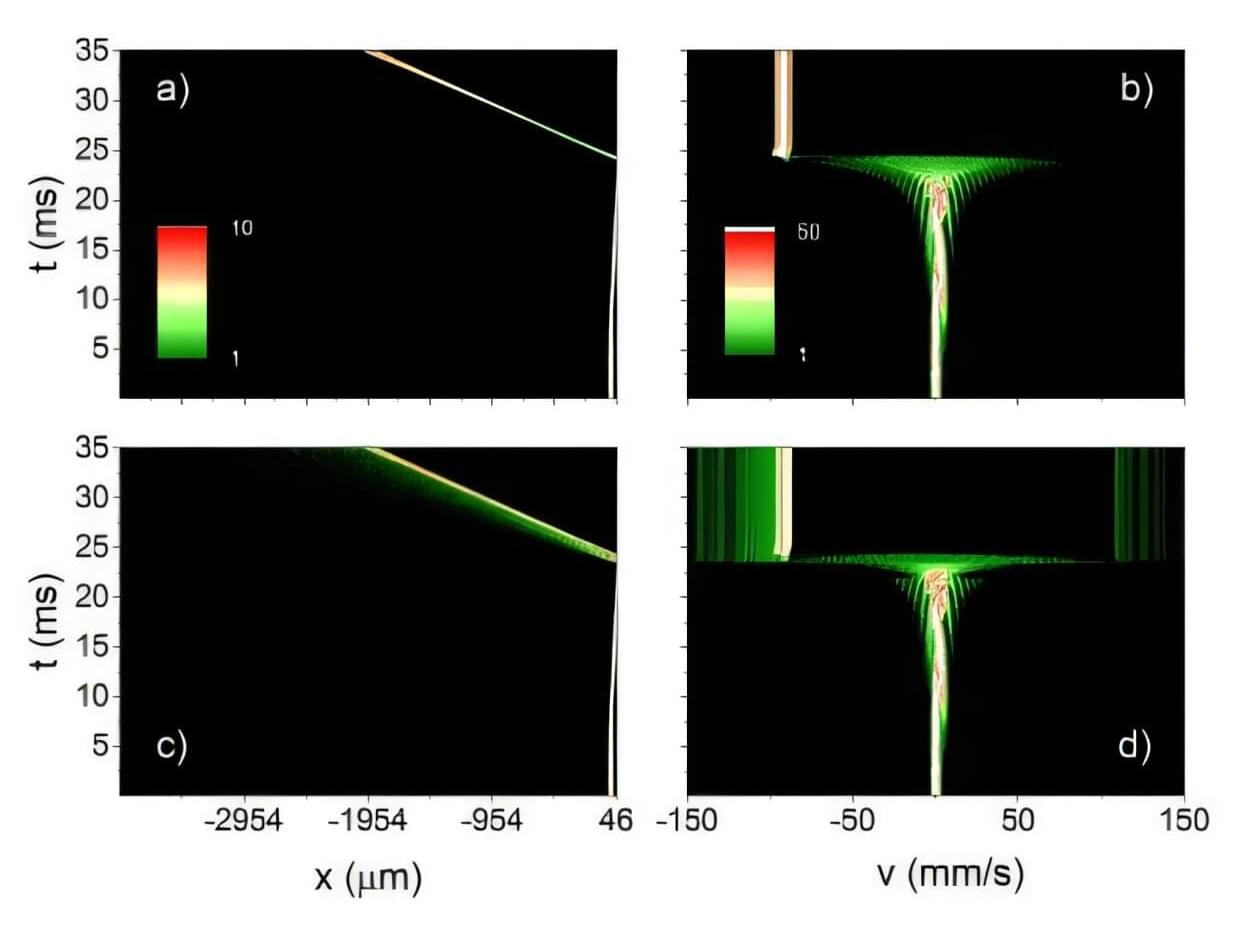
Scientists have used ultracold atoms to successfully demonstrate a novel method of particle acceleration that could unlock a new understanding of how cosmic rays behave, a new study reveals.
More than 70 years after its formulation, researchers have observed the Fermi acceleration mechanism in a laboratory by colliding ultracold atoms against engineered movable potential barriers—delivering a significant milestone in high-energy astrophysics and beyond.
Fermi acceleration is the mechanism responsible for the generation of cosmic rays, as postulated by physicist Enrico Fermi in 1949. The process itself also features some universal properties that have spawned a wide range of mathematical models, such as the Fermi-Ulam model. Until now, however, it has been difficult to create a reliable Fermi accelerator on Earth.