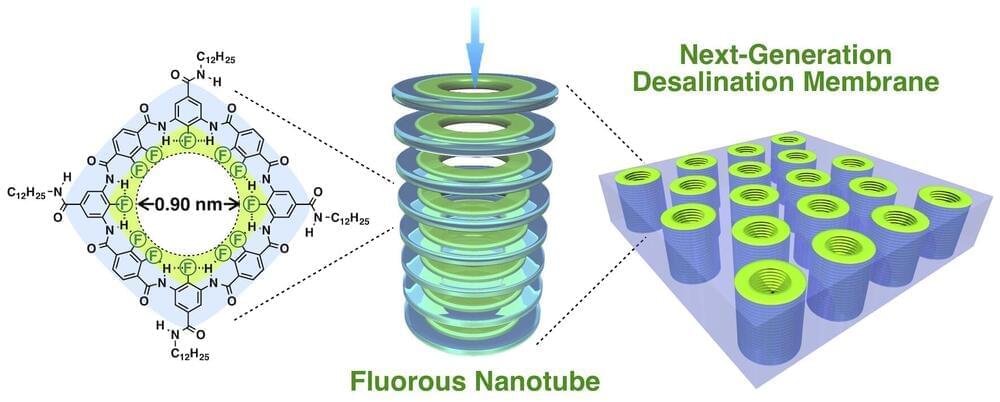
Water scarcity is a growing problem around the world. Desalination of seawater is an established method to produce drinkable water but comes with huge energy costs. For the first time, researchers use fluorine-based nanostructures to successfully filter salt from water. Compared to current desalination methods, these fluorous nanochannels work faster, require less pressure and less energy, and are a more effective filter.
If you’ve ever cooked with a nonstick Teflon-coated frying pan, then you’ve probably seen the way that wet ingredients slide around it easily. This happens because the key component of Teflon is fluorine, a lightweight element that is naturally water repelling, or hydrophobic. Teflon can also be used to line pipes to improve the flow of water. Such behavior caught the attention of Associate Professor Yoshimitsu Itoh from the Department of Chemistry and Biotechnology at the University of Tokyo and his team. It inspired them to explore how pipes or channels made from fluorine might operate on a very different scale, the nanoscale.
“We were curious to see how effective a fluorous nanochannel might be at selectively filtering different compounds, in particular, water and salt. And, after running some complex computer simulations, we decided it was worth the time and effort to create a working sample,” said Itoh. “There are two main ways to desalinate water currently: thermally, using heat to evaporate seawater so it condenses as pure water, or by reverse osmosis, which uses pressure to force water through a membrane that blocks salt. Both methods require a lot of energy, but our tests suggest fluorous nanochannels require little energy, and have other benefits too.”