Quantum information protocols require various types of entanglement, such as Einstein-Podolsky-Rosen, Greenberger-Horne-Zeilinger, and cluster states. In optics, on-demand preparation of these states has been realized by squeezed light sources, but such experiments require different optical circuits for different entangled states, thus lacking versatility. Here, we demonstrate an on-demand entanglement synthesizer that programmably generates all these entangled states from a single squeezed light source. This is achieved by a loop-based circuit that is dynamically controllable at nanosecond time scales and processes optical pulses in the time domain. We verify the generation of five different small-scale entangled states and a large-scale cluster state containing more than 1000 modes without changing the optical circuit. Moreover, this circuit enables storage and release of one part of the generated entangled state, thus working as a quantum memory. Our demonstration should open a way for a more general entanglement synthesizer and a scalable quantum processor.
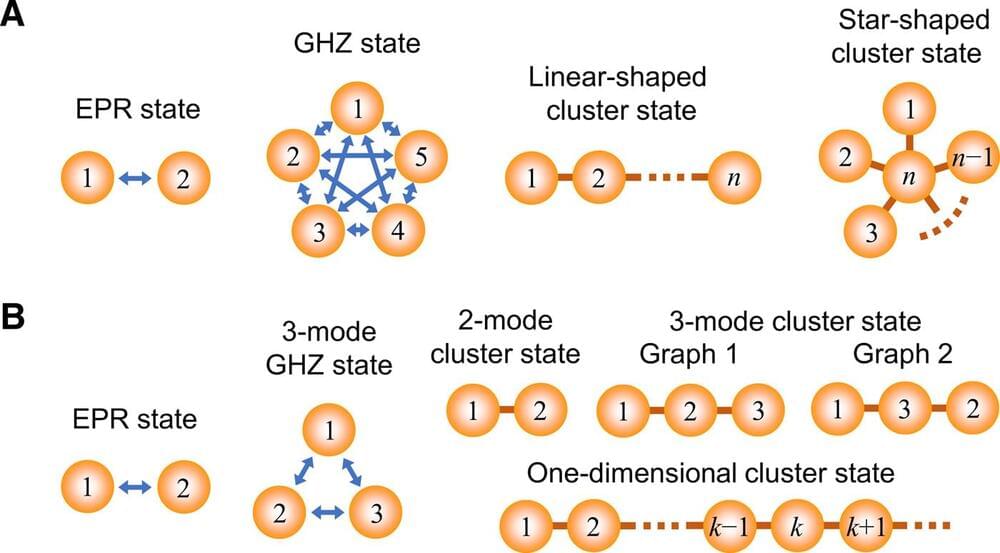
Entanglement is an essential resource for many quantum information protocols in both qubit and continuous variable (CV) regimes. However, different types of entanglement are required for different applications (Fig. 1A). The most commonly used maximally entangled state is a two-mode Einstein-Podolsky-Rosen (EPR) state (1), which is the building block for two-party quantum communication and quantum logic gates based on quantum teleportation (2, 3). Its generalized version is an n-mode Greenberger-Horne-Zeilinger (GHZ) state (4, 5), which is central to building a quantum network; this state, once shared between n parties, enables any two of the n parties to communicate with each other (5, 6). In terms of quantum computation, a special type of entanglement called cluster states has attracted much attention as a universal resource for one-way quantum computation (7–9).